配套作业——分治策略
需求
- 解释分治策略的基本思想,并用它分析大整数相乘问题
- 选做:编程实现大整数相乘问题(选做)
- 编程实现二分搜索,快速排序,棋盘覆盖问题
- 编程实现归并排序,并简述其中的分治策略体现在哪里(选做)
实现
大整数相乘
- 分治策略思想:
- 分:把问题分解成两个或者更小规模的子问题
- 治:利用递归解决子问题
- 合:归并子问题的解得到原问题的解
- 如果用分治策略解大整数相乘问题:
- 把两个整数拆分成四个小整数相乘
- 利用·
AD+BC)=(A+B)*(C+D)-AC-BD替换,将4次乘法运算降低到3次
- 这里的大整数相乘只是着重于降低算法的时间复杂度,并不能真正做到大整数相乘(溢出)
- 要写出真正的大整数相乘,应该用一个字符数组来输入输出数组
- 感兴趣的读者可以参考基础算法二 | Gallifrey’s Blog中高精度乘法,编写真正的两个大整数相乘代码
1 |
|
二分搜索
1 |
|

快速排序
1 |
|

归并排序
1 |
|

棋盘覆盖问题
- 这里的java代码是直接沿用了这篇文章(18条消息) 算法:棋盘覆盖问题怎么取名啊的博客-CSDN博客棋盘覆盖问题,文章里对解题过程做了很详细的解释,感兴趣的读者也可以看一下
- 其实棋盘覆盖问题,如果手写一下过程去解题是很容易理解的,只是代码规模比较大
- 读者可以尝试手画一个8*8的棋盘,手动模拟一下解题是过程,感受分治策略在其中的应用
- 代码中变量解释:
- BOARD_SIZE:方格大小
- board:用于表示棋盘
- title:表示每个L型骨牌的颜色(用数字表示)
- tr:棋盘的行
- tc:棋盘的列
- (tr,tc)始终表示每一个区域的左上角,用于区域划分
- dr:特殊方格所在的行
- dc:特殊方格所在的列
- size:棋盘的边长
1 | public class ChessBoardCoverage { |
- 当然只要轻微修改一下,你就可以获得一份C++的代码
1 |
|
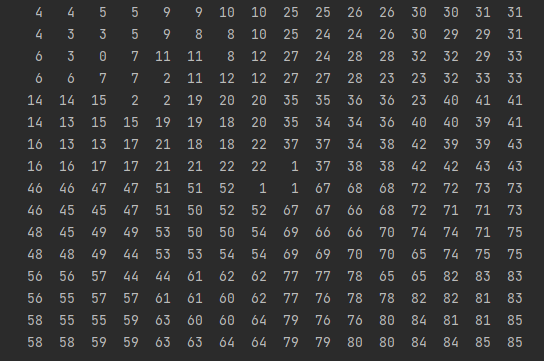
- 从数字的大小能看出棋盘覆盖实现的过程
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Gallifrey的计算机学习日记!
评论


