项目一：迷宫求解

a)需求分析：

要求

可以输入一个任意大小的迷宫数据，用非递归的方法求出一条走出迷宫的路径，并将路径输出

b)概要设计：

思路
  • 我打算设计一个迷宫游戏，用不同的算法生成迷宫，再用不同算法作路径规划
  • 非递归的方法排除dfs路径规划方法
  • 制作成可视化的程序
  • 实现BFS算法寻找迷宫终点

  • 实现基本的地图及寻找路径可视化

    • 实现prim迷宫生成算法
    • 改进BFS算法
    • 独立出地图绘制类，供不同算法使用
    • 封装主地图类

    • 封装节点类

    • 启用Scene Builder工具编写界面-

    • 实现基本的UI界面
    • 封装所有页面，改写为ButtonChose类的方法，实现页面跳转
    • 加入DFS迷宫生成算法
  • 重构MainMap类及其子类
  • 重构bfs寻路算法
  • 加入AStar寻路算法
  • 加入bfs寻路算法
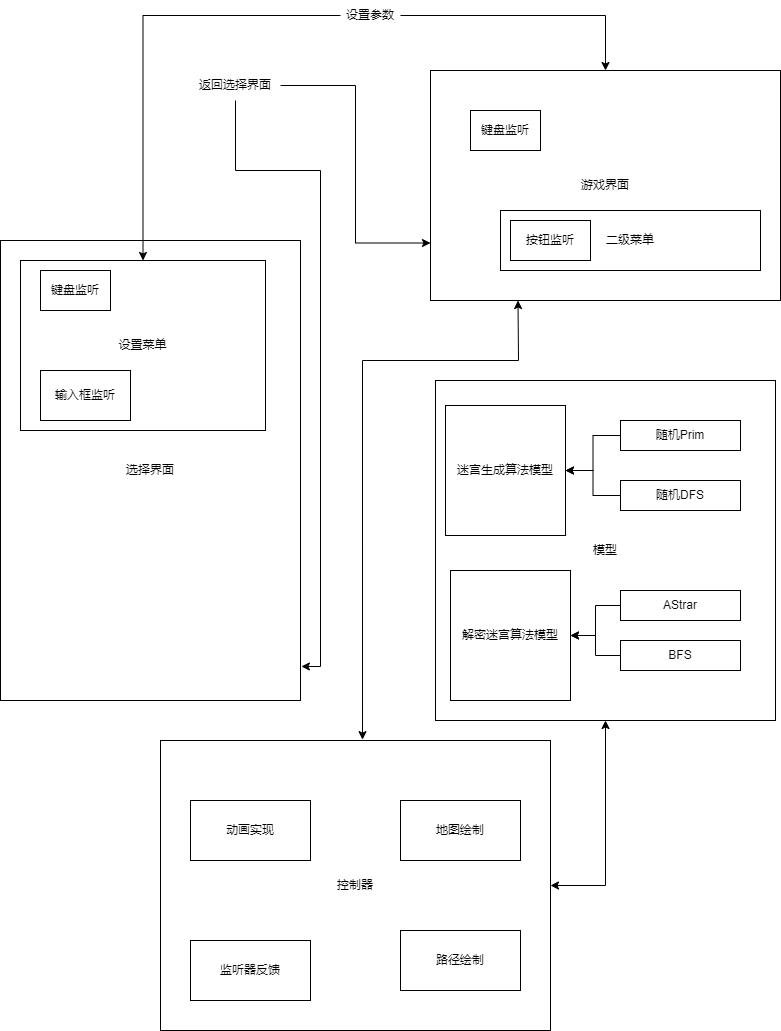
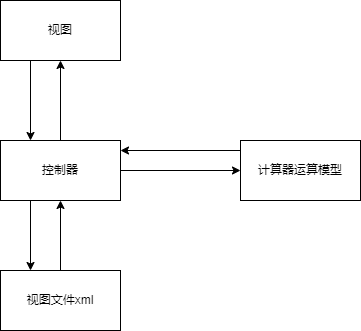
项目整体的设置思路图

io-1

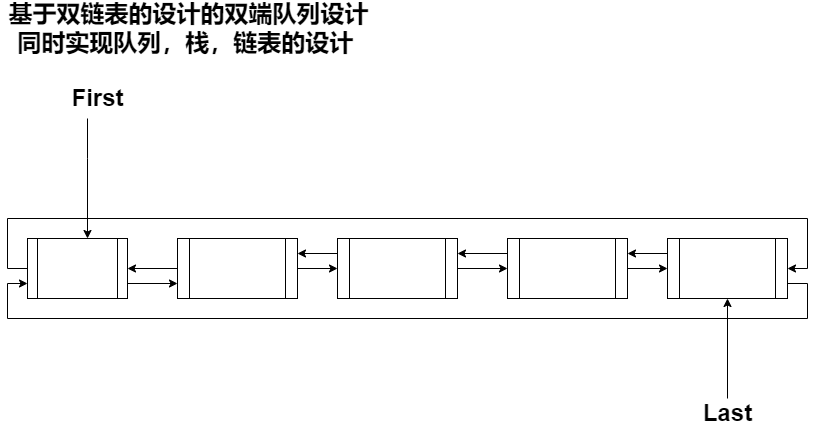
一些数据结构设计图

io6.drawio

io7.drawio

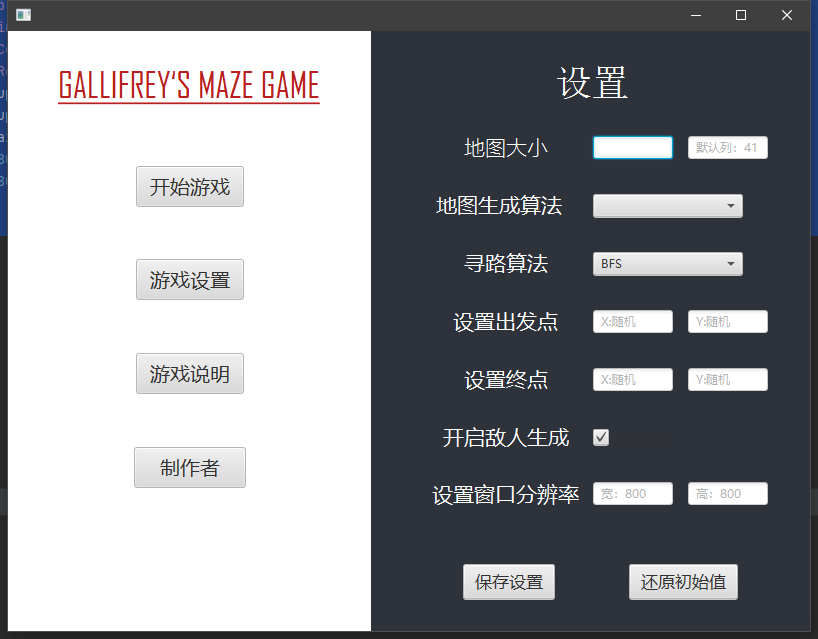
设计说明：

该项目被我设计了一个迷宫游戏，玩家可以通过选择界面对迷宫的大小尺寸，迷宫的生成方式，起点与终点，屏幕分辨率等等属性进行时设置

点击开始游戏后，游戏会根据玩家的设置根据相应算法生成迷宫，玩家可以通过aswd四个键位操作角色走迷宫。

玩家可以通过按键J来使用BFS算法实时实现路径规划（显示角色到终点的路径，实时运算）

玩家可以通过按键L来使用AStar算法实时实现路径规划（显示角色到终点的路径，实时运算）

玩家可以通过按键K来进行角色导航（显示角色到终点的行走动画，实时运算，默认BFS算法）

算法的设计有：
  1. 随机prim迷宫生成算法
  2. 随机dfs迷宫生成算法
  3. AStar路径规划算法
  4. BFS路径规划算法
用到的数据结构有：
  1. 链表
  2. 队列
  3. 双端队列
  4. 栈
  5. 优先队列
  6. 广义表
  7. 数组
  8. 树

c）详细设计：

地图的每个点—Node类的设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
class Node {
    int FValue;//总代价
    int HValue;//预估代价 当前点到终点的的代价
    int GValue;//当前代价 当前点到起点的代价

    int x, y;//x坐标，y坐标
    int pre;//上个节点
    int id = 0;//编号
    boolean isVisited=false;//是否访问
    int value=1;//1是墙，0是路
    public Node(){
    }
    public Node(int x, int y, int pre) {
        this.x = x;
        this.y = y;
        this.pre = pre;

    }
    public Node(int x, int y) {
        this.x = x;
        this.y = y;
    }
    public int getX() {
        return x;
    }
    public void setX(int x) {
        this.x = x;
    }
    public int getY() {
        return y;
    }
    public void setY(int y) {
        this.y = y;
    }
    public int getPre() {
        return pre;
    }
    public void setPre(int pre) {
        this.pre = pre;
    }
    public void setId(int id) {
        this.id = id;
    }
    public int getId() {
        return id;
    }
    public boolean isVisited() {
        return isVisited;
    }
    public void setVisited(boolean visited) {
        isVisited = visited;
    }
    public int getValue() {
        return value;
    }
    public void setValue(int value) {
        this.value = value;
    }
    public void setHValue(Node end) {
           HValue= Math.abs(x-end.getX())+Math.abs(y- end.getY());
    }
    public void setGValue(Node start) {
        //曼哈顿计算G值
        HValue= Math.abs(x-start.getX())+Math.abs(y- start.getY());
    }
    public int getFValue() {
        FValue=HValue+GValue;
        return FValue;
    }

    @Override
    public String toString(){
        return new String(x+" "+y);
    }
}
迷宫生成算法接口的设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
public class MainMap {
    protected Node start;//起点
    protected Node end;//终点
    protected int col;//列数
    protected int row;//行数
    protected Node nodeMap[][];//地图

    public int getCol() {
        return col;
    }

    public void setCol(int col) {
        this.col = col;
    }

    public int getRow() {
        return row;
    }

    public void setRow(int row) {
        this.row = row;
    }

    public MainMap(int col, int row) {
        this.col = col;
        this.row = row;
        nodeMap=new Node[row][col];

    }

    //初始化
    public void InitMap(){
        // 设置全为墙
        for (int i=0;i<row;i++){
            for (int j=0;j< col;j++){
                Node temp=new Node(i,j);
                nodeMap[i][j]=temp;
            }
        }


        /**随机生成起点和终点
         * 避免起点和终点靠得太近，将地图四分起点只在左上生成，终点在右下生成
         * 起点和终点不能同时在边界处
         */
        start=new Node(((int)(Math.random()*row/2+1)),((int)(Math.random()*col/2+1)));
//        System.out.println("开始点"+start.getX()+" "+start.getY());

        end=new Node((int)((Math.random()*row)/2+row/2),(int)((Math.random()*col))/2+col/2);


    }

    public void makeMap(){

    }

    public Node getStart() {
        return start;
    }

    public void setStart(Node start) {
        this.start = start;
    }

    public Node getEnd() {
        return end;
    }

    public void setEnd(Node end) {
        this.end = end;
    }

    public void showMap(){
        System.out.println("起点："+start.getX()+" "+start.getY());
        System.out.println("终点："+end.getX()+" "+end.getY());
        for (int i=0;i<row;i++){
            for (int j=0;j< col;j++){
                System.out.print(nodeMap[i][j].value +" ");
            }
            System.out.println();
        }
    }


    //制作副本
    public MainMap clone(){
        MainMap clone =new MainMap(col,row);
        clone.InitMap();
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){
                clone.nodeMap[i][j].setValue(nodeMap[i][j].getValue());
                clone.nodeMap[i][j].setPre(nodeMap[i][j].getPre());
                clone.nodeMap[i][j].setVisited(nodeMap[i][j].isVisited());
                clone.nodeMap[i][j].setX(nodeMap[i][j].getX());
                clone.nodeMap[i][j].setY(nodeMap[i][j].getY());
                clone.nodeMap[i][j].setId(nodeMap[i][j].getId());
            }
        }
        clone.end=end;
        clone.start=start;
        return clone;
    }

}
地图接口设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
public class MainMap {
    protected Node start;//起点
    protected Node end;//终点
    protected int col;//列数
    protected int row;//行数
    protected Node nodeMap[][];//地图

    public int getCol() {
        return col;
    }

    public void setCol(int col) {
        this.col = col;
    }

    public int getRow() {
        return row;
    }

    public void setRow(int row) {
        this.row = row;
    }

    public MainMap(int col, int row) {
        this.col = col;
        this.row = row;
        nodeMap=new Node[row][col];

    }

    //初始化
    public void InitMap(){
        // 设置全为墙
        for (int i=0;i<row;i++){
            for (int j=0;j< col;j++){
                Node temp=new Node(i,j);
                nodeMap[i][j]=temp;
            }
        }


        /**随机生成起点和终点
         * 避免起点和终点靠得太近，将地图四分起点只在左上生成，终点在右下生成
         * 起点和终点不能同时在边界处
         */
        start=new Node(((int)(Math.random()*row/2+1)),((int)(Math.random()*col/2+1)));
//        System.out.println("开始点"+start.getX()+" "+start.getY());

        end=new Node((int)((Math.random()*row)/2+row/2),(int)((Math.random()*col))/2+col/2);


    }

    public void makeMap(){

    }

    public Node getStart() {
        return start;
    }

    public void setStart(Node start) {
        this.start = start;
    }

    public Node getEnd() {
        return end;
    }

    public void setEnd(Node end) {
        this.end = end;
    }


    public void showMap(){
        System.out.println("起点："+start.getX()+" "+start.getY());
        System.out.println("终点："+end.getX()+" "+end.getY());
        for (int i=0;i<row;i++){
            for (int j=0;j< col;j++){
                System.out.print(nodeMap[i][j].value +" ");
            }
            System.out.println();
        }
    }

    //制作副本
    public MainMap clone(){
        MainMap clone =new MainMap(col,row);
        clone.InitMap();
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){
                clone.nodeMap[i][j].setValue(nodeMap[i][j].getValue());
                clone.nodeMap[i][j].setPre(nodeMap[i][j].getPre());
                clone.nodeMap[i][j].setVisited(nodeMap[i][j].isVisited());
                clone.nodeMap[i][j].setX(nodeMap[i][j].getX());
                clone.nodeMap[i][j].setY(nodeMap[i][j].getY());
                clone.nodeMap[i][j].setId(nodeMap[i][j].getId());
            }
        }
        clone.end=end;
        clone.start=start;
        return clone;
    }
}
路径规划算法接口设计
1
2
3
public interface SF {
    public LinkedList<Node> find3();
}
Prim随机生成地图算法原理与代码

1.让迷宫全是墙.
2.选一个单元格作为迷宫的通路，然后把它的邻墙放入列表
3.当列表里还有墙时
1.从列表里随机选一个墙，如果这面墙分隔的两个单元格只有一个单元格被访问过
1.那就从列表里移除这面墙，即把墙打通，让未访问的单元格成为迷宫的通路
2.把这个格子的墙加入列表
2.如果墙两面的单元格都已经被访问过，那就从列表里移除这面墙

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
public void makeMap(){
    InitMap();
    nodeMap[1][1].setValue(0);//将起点变成路

    LinkedList<Node> listA=new LinkedList<>();
    LinkedList<Node> listB= null;
    int tempR = 0;
    int tempC = 0;
    //待选路点进入链表
    Node temp=nodeMap[1][3];
    listA.add(temp);
    temp=nodeMap[3][1];
    listA.add(temp);

    while (listA.size()!=0){

        int randomNodeId=(int)(listA.size()*Math.random());//随机备选点作为A
        Node randomA=listA.get(randomNodeId);//随机路点A
        listB=new LinkedList<>();
        boolean flag=true;
        //将选路点A四周是路的进入备选池
        for (int i=0;i<4;i++){
            switch (i){
                case 0:tempR=randomA.getX()-2;tempC=randomA.getY();break;
                case 1:tempR=randomA.getX()+2;tempC=randomA.getY();break;
                case 2:tempR=randomA.getX();tempC=randomA.getY()+2;break;
                case 3:tempR=randomA.getX();tempC=randomA.getY()-2;break;
            }
            if(!(tempC<col&&tempC>=0&&tempR>=0&&tempR<row)){
                continue;
            }
            //判断是否通路    加入临时通路备选池B
            if(nodeMap[tempR][tempC].getValue()==0){
                temp=nodeMap[tempR][tempC];
                listB.add(temp);// listB其实用数组更好 ，大小只有0-3 有1个是来的点，肯定访问过了
            }
            //判断是否为墙和A中是否包含该点加入 待选路点链表listA
            else if(nodeMap[tempR][tempC].getValue()==1&&!listA.contains(nodeMap[tempR][tempC])){
                    temp=nodeMap[tempR][tempC];
                    listA.add(temp);
            }
        }

        int randomPass=(int)(listB.size()*Math.random());//随机备选点作为B
        Node randomB=listB.get(randomPass);//随机通路点
        //打通一条通路
        nodeMap[randomA.getX()][randomA.getY()].setValue(0);
        nodeMap[(randomB.getX()+randomA.getX())>>1][(randomA.getY()+randomB.getY())>>1].setValue(0);
        listA.remove(randomA);
    }

    //确保生成一个可达的终点
    while (nodeMap[end.getX()][end.getY()].getValue()==1){
        end=new Node((int)((Math.random()*row)/2+row/2),(int)((Math.random()*col))/2+col/2);
    }
}
DFS随机生成地图算法原理与代码

1.将起点作为当前迷宫单元并标记为已访问
2.当还存在未标记的迷宫单元，进行循环
1.如果当前迷宫单元有未被访问过的的相邻的迷宫单元
1.随机选择一个未访问的相邻迷宫单元
2.将当前迷宫单元入栈
3.移除当前迷宫单元与相邻迷宫单元的墙
4.标记相邻迷宫单元并用它作为当前迷宫单元
2.如果当前迷宫单元不存在未访问的相邻迷宫单元，并且栈不空
1.栈顶的迷宫单元出栈
2.令其成为当前迷宫单元

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
    public void makeMap(){
        InitMap();
        LinkedList<Node> stackList=new LinkedList<>();

//        1.将起点作为当前迷宫单元并标记为已访问
        Node current=nodeMap[1][1];
        nodeMap[1][1].setVisited(true);
        stackList.add(current);

//        2.当还存在未标记的迷宫单元，进行循环
        while(stackList.size()!=0) {

            //遍历4个方向
            int tempR=0;
            int tempC=0;
            LinkedList<Node> AdjList=new LinkedList<>();
            for(int i=0;i<4;i++){
                switch (i){
                    case 0:tempR=current.getX()-2;tempC=current.getY();break;
                    case 1:tempR=current.getX()+2;tempC=current.getY();break;
                    case 2:tempR=current.getX();tempC=current.getY()+2;break;
                    case 3:tempR=current.getX();tempC=current.getY()-2;break;
                }
                //处理边界问题
                if(!(tempC<col&&tempC>0&&tempR>0&&tempR<row)){
                    continue;
                }
                //未访问过的进入选择
                if(nodeMap[tempR][tempC].isVisited==false){
                   AdjList.add(nodeMap[tempR][tempC]);
                }
            }
//          1.如果当前迷宫单元有未被访问过的的相邻的迷宫单元
            if(AdjList.size()!=0) {
//              1.随机选择一个未访问的相邻迷宫单元
                int randomDir = (int) ((AdjList.size() * Math.random()));
                Node adjNode = AdjList.get(randomDir);
//              2.将当前迷宫单元入栈
                stackList.push(current);
//              3.移除当前迷宫单元与相邻迷宫单元的墙
                adjNode.setValue(0);
                current.setValue(0);
                nodeMap[(adjNode.getX()+current.getX())>>1][(adjNode.getY()+current.getY())>>1].setValue(0);
                nodeMap[(adjNode.getX()+current.getX())>>1][(adjNode.getY()+current.getY())>>1].setVisited(true);

//              4.标记相邻迷宫单元并用它作为当前迷宫单元
                adjNode.setVisited(true);
                current=adjNode;

            }
//          2.如果当前迷宫单元不存在未访问的相邻迷宫单元，并且栈不空
            if(stackList.size()!=0&&AdjList.size()==0) {
//              1.栈顶的迷宫单元出栈
//              2.令其成为当前迷宫单元
                 current=stackList.pop();
            }
        }
        //确保生成一个可达的终点
        while (nodeMap[end.getX()][end.getY()].getValue()==1){
            end=new Node((int)((Math.random()*row)/2+row/2),(int)((Math.random()*col))/2+col/2);
        }
    }
BFS路径规划算法原理及代码

从迷宫的入口开始，进行层次优先遍历（BFS，我更喜欢称之为层次优先遍历，因为这样更形象）。BFS遍历的关键就是需要用到一个队列，在这道题中，只需要从入口点出发，依次看下它的上下左右四个结点是否可以走，如果可以走，就立即把这个结点push到队列尾部，然后每次找的时候就是从队头取出一个点，依次看它的上下左右四个方向。遍历的路径的时候注意是从出口往入口找，所以需要用到一个栈保存一下路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
//查找
public boolean find(){
    Node start= mainMap.getStart();
    Node end=mainMap.getEnd();
    start.setPre(-1);
    nodeMap =mainMap.nodeMap;

    linkedList=new LinkedList<>();
    Node temp=null;
    linkedList.offer(start);
    rear++;
    nodeMap[start.getX()][start.getY()].setValue(-1);
    while(!(front==rear)) {
        temp=linkedList.get(++front);
        //判断是不是终点
        if (temp.getX() ==end.getX() && temp.getY() ==end.getY()) {
            return true;
        }
        //遍历4个方向

        Node temp2 = null;
        for (int i = 0; i < 4; i++) {
            switch (i) {
                case 0:
                    temp2 = new Node(temp.x, temp.y - 1);
                    break;
                case 1:
                    temp2 = new Node(temp.x, temp.y + 1);
                    break;
                case 2:
                    temp2 =  new Node(temp.x - 1, temp.y);
                    break;
                case 3:
                    temp2 = new Node(temp.x + 1, temp.y);
                    break;
            }
            //可走进队
            if (temp2.getX()<mainMap.getCol()&&temp2.getX()>0&&temp.getY()>0&&temp2.getY()<mainMap.getRow()&&nodeMap[temp2.getX()][temp2.getY()].getValue()==0) {

                linkedList.offer(temp2);
                rear++;
                temp2.id=linkedList.indexOf(temp2);
                temp2.setPre(temp.getId());
                nodeMap[temp2.getX()][temp2.getY()].setValue(-1);
            }
        }
    }

    return false;
}

public  boolean find2(){
    linkedList2=new LinkedList<>();
    linkedList2.add(linkedList.get(front));
    int j=0;
    while (linkedList2.get(j).getPre()!=-1){
        linkedList2.add(linkedList.get(linkedList2.get(j).getPre()));
        j++;
    }
    linkedList=linkedList2;
    return true;
}

public LinkedList<Node> find3(){

    long time1=new Date().getTime();
    System.out.println(time1);
    find();
    find2();

    long time2=new Date().getTime();
    System.out.println(time2);
    System.out.println(time2-time1);
    return linkedList;
}

AStar路径规划算法原理及代码

1.起点先添加到开启列表中
2.开启列表中有节点的话，取出第一个节点，即最小F值的节点
判断此节点是否是目标点，是则找到了，跳出
根据此节点取得四个方向的节点，求出G，H，F值
判断每个节点在地图中是否能通过，不能通过则加入关闭列表中，跳出
判断每个节点是否在关闭列表中，在则跳出
判断每个节点是否在开启列表中，在则更新G值，F值，还更新其父节点；不在则将其添加到开启列表中，计算G值，H值，F值，添加其节点
3.把此节点从开启列表中删除，再添加到关闭列表中
4.把开启列表中按照F值最小的节点进行排序，最小的F值在第一个
5.重复2，3，4步骤

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
    public void find(){

        //建立一个优先队列
        open=new PriorityQueue<>(NodeComparator);
        //建一个保存链表
        keptList=new LinkedList<>();


        //起点的当前代价为0 预估代价用曼哈顿公式算
        start=mainMap.getStart();
        start.setPre(-1);
        nodeMap[start.getX()][start.getY()].setValue(-1);
        start.setGValue(start);
        start.setHValue(end);

        open.add(start);
//      开启列表中有节点的话，取出第一个节点，即最小F值的节点

//        int GValue=1;

        while(open.size()!=0){
            Node current=open.poll();

            keptList.offer(current);//保存下来，就可以找到路径了
            current.id=keptList.indexOf(current);
//            判断此节点是否是目标点，是则找到了，跳出
            if(current.getX()==end.getX()&&current.getY()==end.getY()) {break;}


            //遍历4个方向

            Node temp2 = null;
            for (int i = 0; i < 4; i++) {
                switch (i) {
                    case 0:
                        temp2 = new Node(current.x, current.y - 1);
                        break;
                    case 1:
                        temp2 = new Node(current.x, current.y + 1);
                        break;
                    case 2:
                        temp2 =  new Node(current.x - 1, current.y);
                        break;
                    case 3:
                        temp2 = new Node(current.x + 1, current.y);
                        break;
                }
                //可走进队
                if (temp2.getX()<mainMap.getCol()&&temp2.getX()>0&&temp2.getY()>0&&temp2.getY()<mainMap.getRow()&&nodeMap[temp2.getX()][temp2.getY()].getValue()==0) {

                    //将四周的点都加入优先队列 算出所有FValue
                    temp2.setGValue(start);
                    temp2.setHValue(end);

                    temp2.setPre(current.getId());
                    nodeMap[temp2.getX()][temp2.getY()].setValue(-1);
                    open.add(temp2);
                }
            }

        }



    }

    public  boolean find2(){
        LinkedList<Node>linkedList2=new LinkedList<>();
        linkedList2.add(keptList.getLast());
        int j=0;
        while (linkedList2.get(j).getPre()!=-1){
            linkedList2.add(keptList.get(linkedList2.get(j).getPre()));
            j++;
        }
        keptList=linkedList2;
        return true;
    }
    public LinkedList<Node> find3(){
        long time1=new Date().getTime();
        System.out.println(time1);
        find();
        find2();

        long time2=new Date().getTime();
        System.out.println(time2);
        System.out.println(time2-time1);
        return keptList;
    }

绘图接口设计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
package com.gallifrey.mazegame4;

import javafx.scene.Group;

public class MainPrint {
    protected Group group;
    protected MainMap mainMap;
    protected double OneCol;
    protected double OneRow;
    public MainPrint(Group group,MainMap mainMap) {
        this.group = group;
        this.mainMap = mainMap;
        OneCol=(double) 800 / mainMap.getCol();
        OneRow=(double) 800/mainMap.getRow();
    }
}

d）调试分析

开始界面（选择界面）

image-20220106044727148

Prim算法随机生成41*41迷宫

image-20220106044954737

DFS算法随机生成41*41迷宫

image-20220106045220105

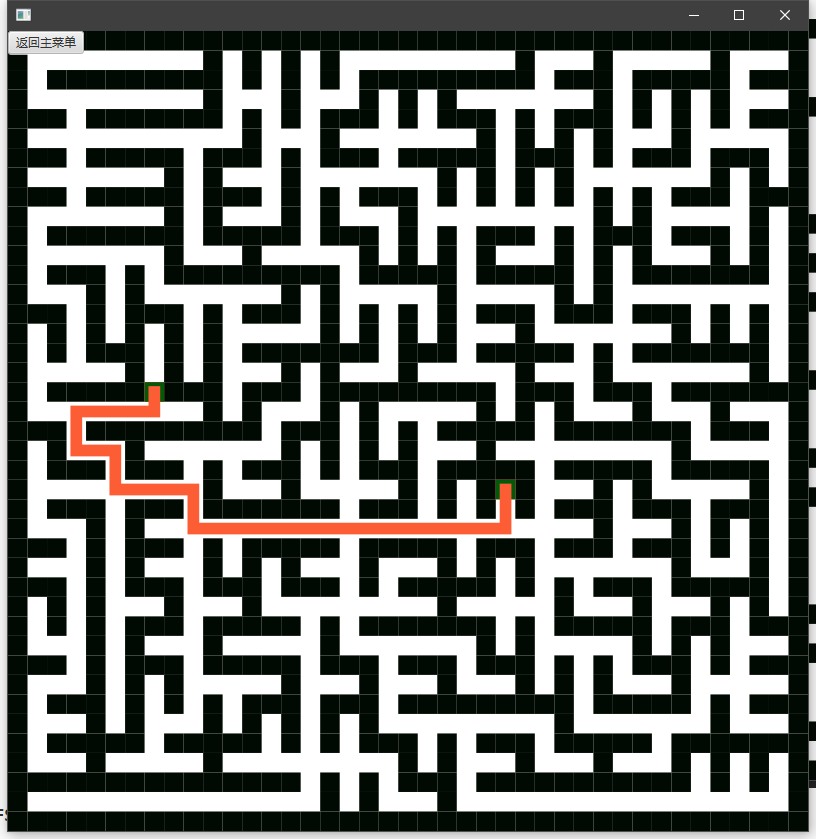
路径规划（解迷宫）

image-20220106045336440

image-20220106045056685

角色导航

image-20220106051028359

时间复杂度

prim迷宫生成算法：原：O(n²)，使用优先队列改进：O(mlogn)

DFS迷宫生成算法：O(n²)

BFS路径规划算法：O(n²)

AStar路径规划算法：O（m*n）;m,n分别是地图的行数和列数

项目二：手写计算器

a)需求分析：

要求

利用计算器实现一元多项式计算，表达式求值是实现程序设计语言的基本问题之一，栈的应用。设计一个程序，演示用算符优先法对算术表达式求值的过程。

该计算器可以进行加减乘除，求余，阶乘，次方根的一元多项式计算

b)概要设计：

思路
  • 利用栈将输入的算术式（中缀表达式）转逆波兰式（后缀表达式）
  • 利用逆波兰式借助栈进行运算
  • 实现基本的可视化以及用户交互功能
整体设计思路图

io2.drawio

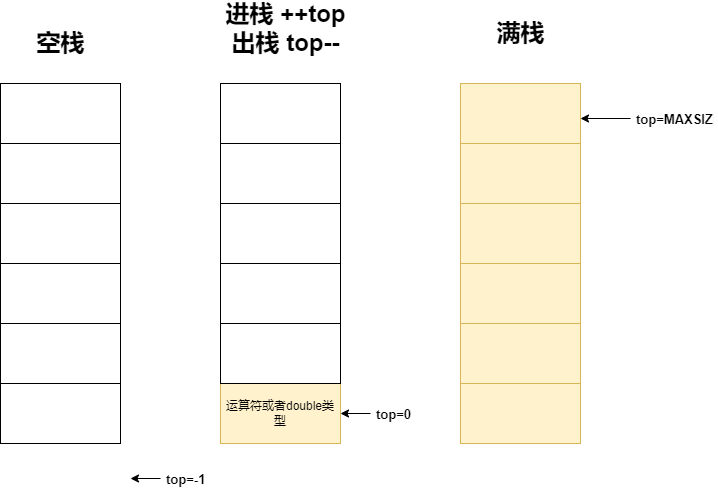
存储结构的设计

io3.drawio

c）详细设计：

栈设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
/**
 * 手写栈
 */
public class MyStack<E> {
    private int MaxSize=1010;
    private E data[];//泛型+强制类型转换
    private int top=-1;//栈顶指针

    public MyStack() {
        data=(E[])new Object[MaxSize];
    }

    //判断是否栈空
    public boolean isEmpty(){
        return (top==-1);
    }

    //进栈
    public void push(E e){
        if(top==MaxSize-1){
            System.out.println("栈满了");
            return;
        }
        data[++top]=e;
    }

    //出栈
    public E pop(){
        if(top==-1){
            System.out.println("栈空");
            return null;
        }
        return data[top--];
    }

    //取栈顶符号
    public E getTop(){
        if(top==-1){
            System.out.println("栈空");
            return null;
        }
        return data[top];
    }
}
逆波兰式算法的实现

将一个普通的中缀表达式转换为逆波兰表达式的一般算法是：

首先需要分配2个栈，一个作为临时存储运算符的栈S1（含一个结束符号），一个作为存放结果（逆波兰式）的栈S2（空栈），S1栈可先放入优先级最低的运算符#，注意，中缀式应以此最低优先级的运算符结束。可指定其他字符，不一定非#不可。从中缀式的左端开始取字符，逐序进行如下步骤：

（1）若取出的字符是操作数，则分析出完整的运算数，该操作数直接送入S2栈。

（2）若取出的字符是运算符，则将该运算符与S1栈栈顶元素比较，如果该运算符(不包括括号运算符)优先级高于S1栈栈顶运算符（包括左括号）优先级，则将该运算符进S1栈（或者栈空），否则，将S1栈的栈顶运算符弹出，送入S2栈中，直至S1栈栈顶运算符（包括左括号）低于（不包括等于）该运算符优先级时停止弹出运算符，最后将该运算符送入S1栈。

（3）若取出的字符是“（”，则直接送入S1栈顶。

（4）若取出的字符是“）”，则将距离S1栈栈顶最近的“（”之间的运算符，逐个出栈，依次送入S2栈，此时抛弃“（”。

（5）重复上面的1~4步，直至处理完所有的输入字符。

（6）若取出的字符是“#”，则将S1栈内所有运算符（不包括“#”），逐个出栈，依次送入S2栈。

计算方法的实现

新建一个表达式,如果当前字符为变量或者为数字，则压栈，如果是运算符，则将栈顶两个元素弹出作相应运算，结果再入栈，最后当表达式扫描完后，栈里的就是结果。

计算器代码的设计:逆波兰式+计算方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
public class Calculator {
    int State;
    MyStack <Character>tempStack;//符号栈 临时栈
    MyStack <Character>outStack2;//    输出栈
    MyStack <String> coutStack;// 运算栈
    String stringArr[];//字符串数组
    int j;
    String suffix;


    public Calculator() {
        tempStack=new MyStack<>();
        outStack2=new MyStack<>();
        coutStack=new MyStack<>();
        suffix=new String();
        stringArr=new String[25];

    }

    //获取优先级
    public int getState(char c){
        if (c == '+' || c == '-') {
             return 1;
        }
        else if (c == '*' || c == '/') {
            return 2;
        }
        else if (c == '%' || c == '^') {
            return 3;
        }
        else if (c == '!') {
            return 4;
        }
        else {
            return 0;
        }
    }

    public void getSuffix(char[] input){
        int i=0;
        while(input[i]!='\0') {
            //数字直接进输出栈
            if(input[i]>='0'&&input[i]<='9'){

                outStack2.push(input[i++]);

            }
            //处理运算符
            else if(input[i]=='+'||input[i]=='-'||input[i]=='*'||input[i]=='/'||input[i]=='!'||input[i]=='%'||input[i]=='^'){
                //如果该运算符(不包括括号运算符)优先级高于tempStack栈栈顶运算符（包括左括号）优先级(或者栈空)，则将该运算符进tempStack栈
                if(tempStack.isEmpty()||tempStack.getTop()=='('||getState(input[i])>getState(tempStack.getTop())){
                    tempStack.push(input[i++]);
                }else {
                //否则，将tempStack栈的栈顶运算符弹出，送入outStack栈中，直至tempStack栈栈顶运算符（包括左括号）低于（不包括等于）该运算符优先级时停止弹出运算符，最后将该运算符送入outStack栈
                    while(!tempStack.isEmpty()&&getState(input[i])<getState(tempStack.getTop())){
                        outStack2.push(tempStack.pop());
                    }
                    outStack2.push(tempStack.pop());
                }
            }
            //若取出的字符是'('，则直接入tempStack栈。
            if (input[i]=='('){
                tempStack.push(input[i]);
            }
            //若取出的字符是')'，tempStack一直出栈到outStack栈中直到遇到 '(',将'('丢弃
            if (input[i]==')'){
                while(tempStack.getTop()!='('){
                    outStack2.push(tempStack.pop());
                }
                tempStack.pop();
            }
        }

        while (!tempStack.isEmpty()){
            outStack2.push(tempStack.pop());
        }
    }

    public String getSuffix(String input){
        suffix=new String();

        for(int i=0;i<input.length();i++){
            //数字直接进输出栈 将数字变成浮点数类型
            if(input.charAt(i)>='0'&&input.charAt(i)<='9'||input.charAt(i)=='.'){
                suffix += input.charAt(i);

                String temp=new String();
                temp += input.charAt(i);

                while (i+1<input.length()&&input.charAt(i+1)>='0'&&input.charAt(i+1)<='9'||i+1<input.length()&&input.charAt(i+1)=='.') {
                    suffix += input.charAt(i+1);
                    temp += input.charAt(i+1);
                    i++;
                }
                stringArr[j++]=temp;


            }
            //处理运算符
             else if(input.charAt(i)=='+'||input.charAt(i)=='-'||input.charAt(i)=='*'||input.charAt(i)=='/'||input.charAt(i)=='!'||input.charAt(i)=='%'||input.charAt(i)=='^'){
                //如果该运算符(不包括括号运算符)优先级高于tempStack栈栈顶运算符（包括左括号）优先级(或者栈空)，则将该运算符进tempStack栈
                if(tempStack.isEmpty()||tempStack.getTop()=='('||getState(input.charAt(i))>getState(tempStack.getTop())){
                    tempStack.push(input.charAt(i));

                }else {
                    //否则，将tempStack栈的栈顶运算符弹出，送入outStack栈中，直至tempStack栈栈顶运算符（包括左括号）低于（不包括等于）该运算符优先级时停止弹出运算符，最后将该运算符送入outStack栈
                    while(!tempStack.isEmpty()&&getState(input.charAt(i))<getState(tempStack.getTop())){
                        stringArr[j++]= String.valueOf(tempStack.getTop());
                        suffix+=tempStack.pop();

                    }
                    tempStack.push(input.charAt(i));
                }
            }
            //若取出的字符是'('，则直接入tempStack栈。
            else if (input.charAt(i)=='('){
               tempStack.push(input.charAt(i));
            }
            //若取出的字符是')'，tempStack一直出栈到outStack栈中直到遇到 '(',将'('丢弃
            else if (input.charAt(i)==')'){
                while(tempStack.getTop()!='('){
                    stringArr[j++]= String.valueOf(tempStack.getTop());
                    suffix+=(tempStack.pop());

                }
                tempStack.pop();
            }
        }

        while (!tempStack.isEmpty()){
            stringArr[j++]= String.valueOf(tempStack.getTop());
            suffix+=(tempStack.pop());

        }


        return suffix;
    }


    /**
     * 新建一个表达式,如果当前字符为变量或者为数字，则压栈，如果是运算符，则将栈顶两个元素弹出作相应运算，结果再入栈，最后当表达式扫描完后，栈里的就是结果
     * @return
     */
    public double getResult(){
        double result;
        for (int i=0;i<j;i++){
                if(stringArr[i].equals("+")){
                    double A= Double.parseDouble(coutStack.pop());
                    double B= Double.parseDouble(coutStack.pop());
                    double C= B+A;
                    coutStack.push(String.valueOf(C));
                }else if(stringArr[i].equals("-")){
                    double A= Double.parseDouble(coutStack.pop());
                    double B= Double.parseDouble(coutStack.pop());
                    double C= B-A;
                    coutStack.push(String.valueOf(C));
                }else if(stringArr[i].equals("*")){
                    double A= Double.parseDouble(coutStack.pop());
                    double B= Double.parseDouble(coutStack.pop());
                    double C= B*A;
                    coutStack.push(String.valueOf(C));
                }else if(stringArr[i].equals("/")){
                    double A= Double.parseDouble(coutStack.pop());
                    double B= Double.parseDouble(coutStack.pop());
                    double C= B/A;
                    coutStack.push(String.valueOf(C));
                }else if(stringArr[i].equals("!")){
                    int A= Integer.parseInt(coutStack.pop());
                    int B=1;
                    while (A!=1){
                        B=B*A;
                        A--;
                    }
                    coutStack.push(String.valueOf(B));
                }else if(stringArr[i].equals("%")){
                    double A= Double.parseDouble(coutStack.pop());
                    double B= Double.parseDouble(coutStack.pop());
                    double C= B%A;
                    coutStack.push(String.valueOf(C));
                }else if(stringArr[i].equals("^")){
                    double A= Double.parseDouble(coutStack.pop());
                    double B= Double.parseDouble(coutStack.pop());
                    double C= Math.pow(B,A);
                    coutStack.push(String.valueOf(C));



                } else{
                    coutStack.push(stringArr[i]);
                }
            }
        result= Double.parseDouble(coutStack.pop());


        return result;
    }

}

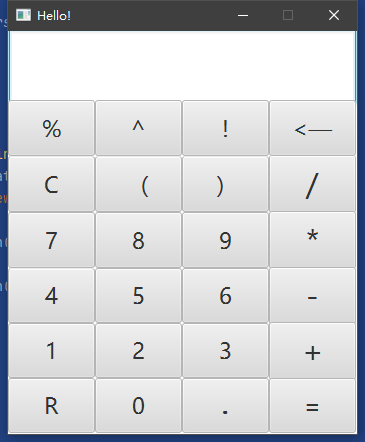
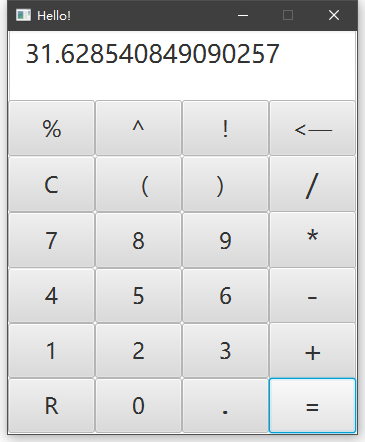
d）调试分析

界面展示

image-20220106054907661

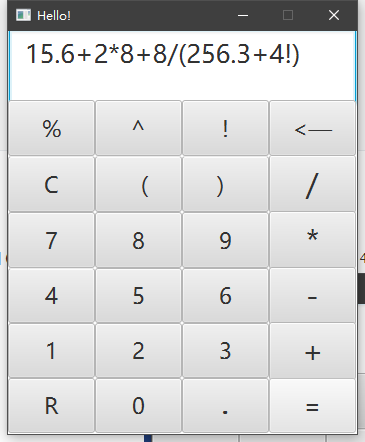
一元多项式运算

image-20220106055136813

image-20220106055637698

项目三：猴子选大王&Joseph环—可视化

a)需求分析：

joseph

编号是1，2，„„,n的n个人按照顺时针方向围坐一圈，每个人只有一个密码（正整数）。一开始任选一个正整数作为报数上限值m,从第一个仍开始顺时针方向自1开始顺序报数，报到m时停止报数。报m的人出列，将他的密码作为新的m值，从他在顺时针方向的下一个人开始重新从1报数，如此下去，直到所有人全 部出列为止。设计一个程序来求出出列顺序

猴子选大王

n只猴子围坐成一个圈，按顺时针方向从1到n编号。然后从1号猴子开始沿顺时针方向从1开始报数，报到m的猴子出局，再从刚出局猴子的下一个位置重新开始报数，如此重复，直至剩下一个猴子，它就是大王。设计并编写程序，实现如下功能：（1） 要求由用户输入开始时的猴子数n、报数的最后一个数m。（2） 给出当选猴王的初始编号。

b)概要设计：

思路

因为这两个题目比较相近，我写了在一起了，用一个可自定义的大小循环队列的解决一次解决，并将此过程可视化，添加用户交互。

整体设计思路图

io4.drawio

在此说明每个部分的算法设计说明（可以是描述算法的流程图），每个程序中使用的存储结构设计说明（如果指定存储结构请写出该存储结构的定义）。

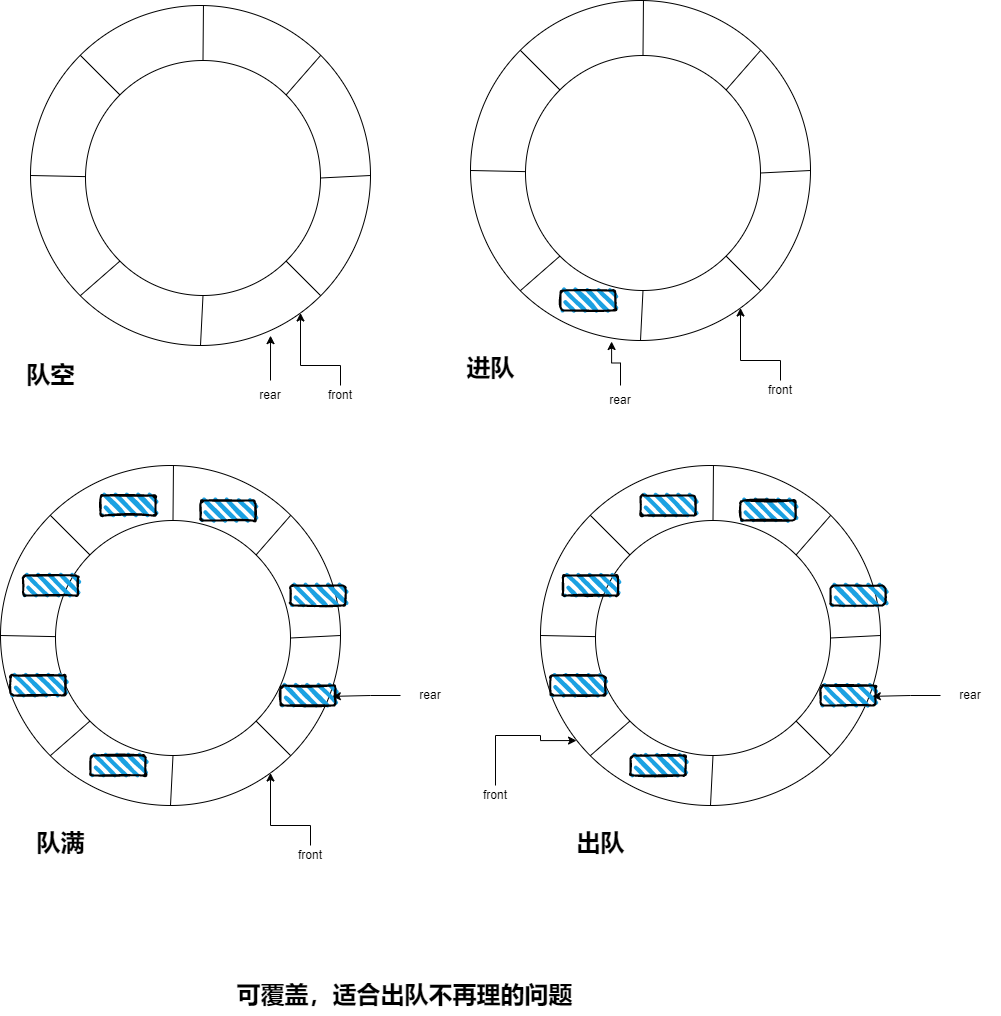
存储结构的设计

io5.drawio

c）详细设计：

循环队列设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
package com.example.moneyking;

/**
 *
 * 手写循环队列
 *
 * @param <E>
 */

public class MySqQueue<E> {

    int Size;//指定大小
    E data[];//泛型+强制类型转换
    int rear=0;
    int front=0;
    int length=0;

    public MySqQueue() {
        Size=(int)1e6;
        data=(E[])new Object[Size];
    }

    public MySqQueue(int size) {
        this.Size = size;
        data=(E[])new Object[Size];
    }

    //判断是否为空
    public boolean isEmpty() {
        return front==rear&&length==0;
    }

    //进队
    public boolean enqueue(E e) {
        if((rear+1)%Size==front){
            System.out.println("队满了");
            return false;
        }
        data[rear] = e;                //进队
        rear = (rear+1)%Size;          //尾指针+1
        length++;                       //长度+1
        return true;
    }

    //出队
    public E dequeue() {
        if(isEmpty()){
            System.out.println("队列为空");
            return null;
        }
        E e = data[front];          //出队元素
        front = (front+1)%data.length; //头指针+1
        length--;                 //长度-1
        return e;
    }

}
算法设计
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void show(){
    MySqQueue<Integer> sqQueue=new MySqQueue<>(MoneyNumber+1);
    //给每个猴子从1到n编号 全部进队
    for(int i=0;i<MoneyNumber;i++){
        sqQueue.enqueue(i+1);
    }

    //定义一个计数器
    int count=0;
    while(!sqQueue.isEmpty()){
        int temp=sqQueue.dequeue();//非空出队
        System.out.print(temp+" ");//输出
        count++;//计数器+1
        if(count==index){
            System.out.println("-------"+temp+"出局");
           count=0;
        }else if(!sqQueue.isEmpty()){
            sqQueue.enqueue(temp);
        }
    }
}

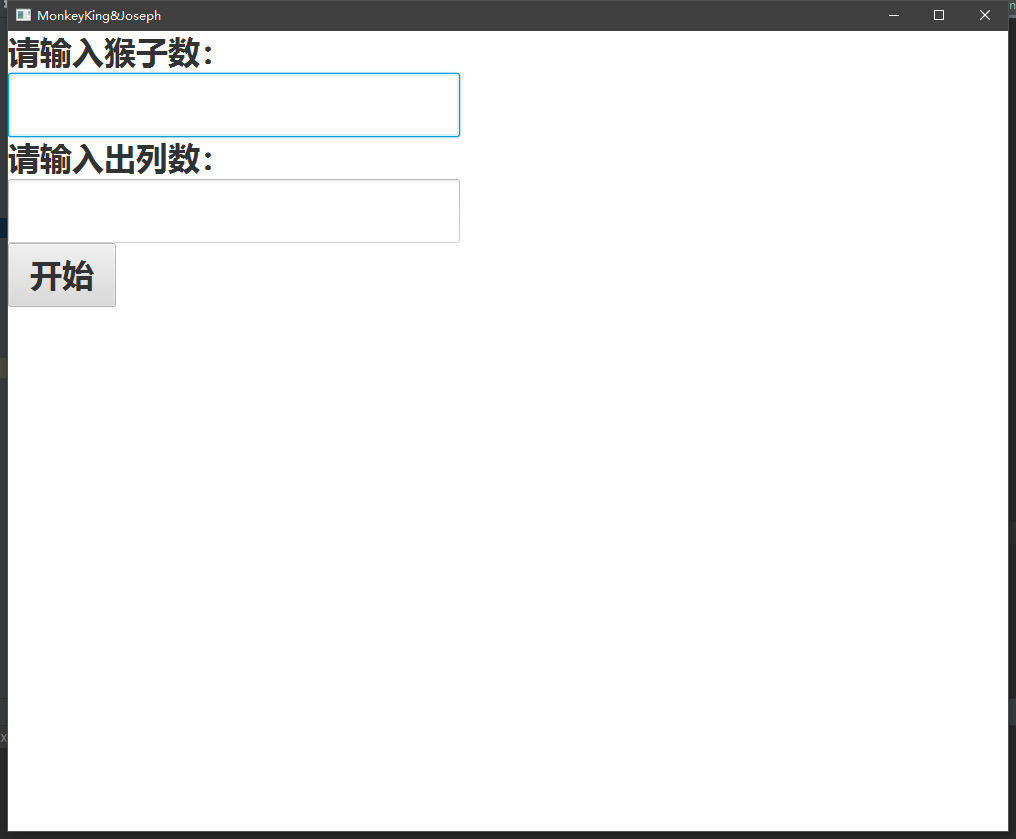
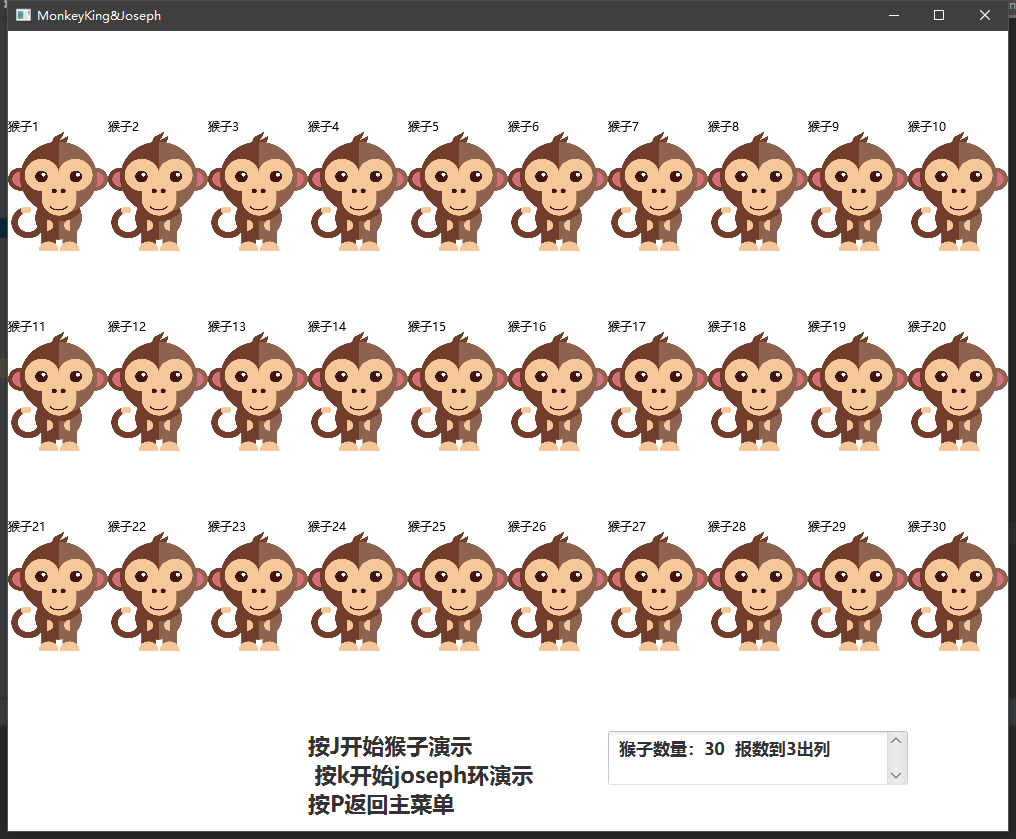
d）调试分析

设置界面

image-20220106063719254

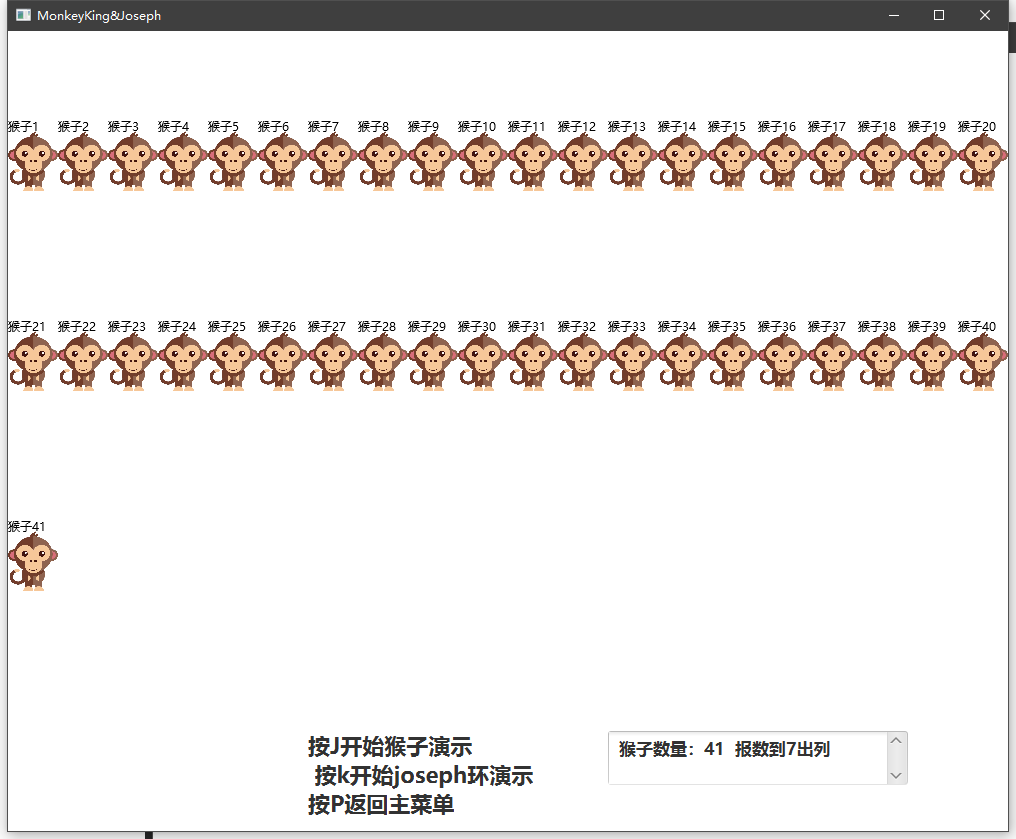
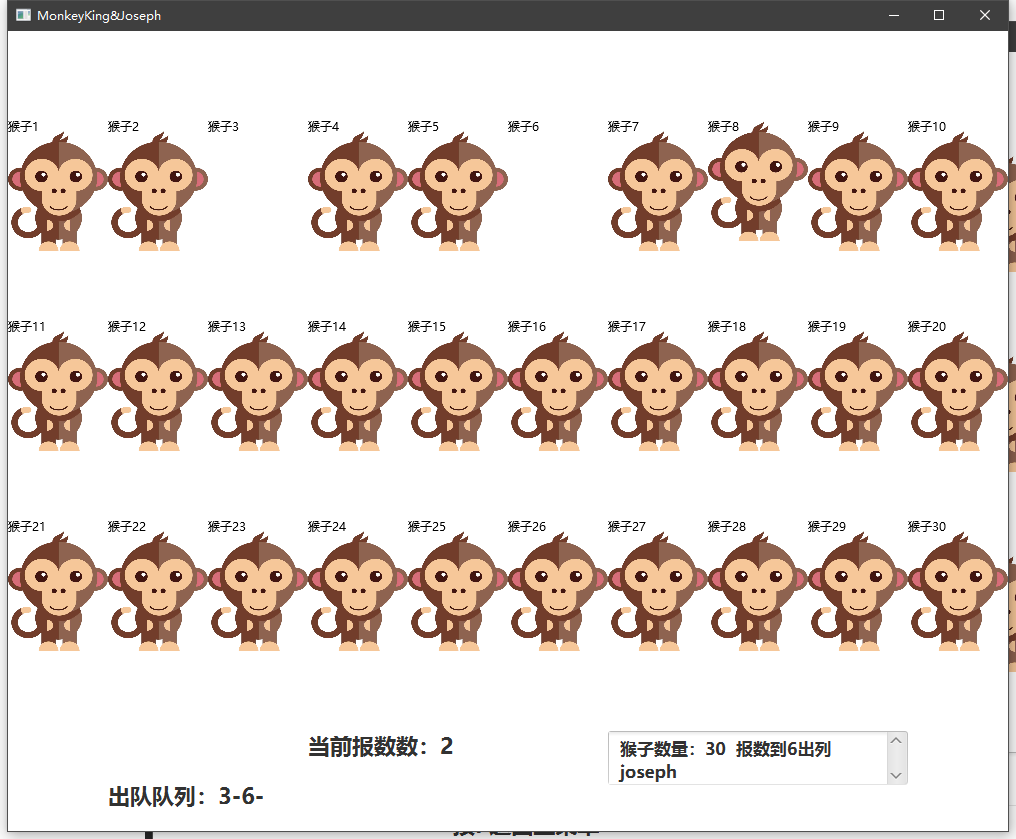
猴子选大王

image-20220106063752608

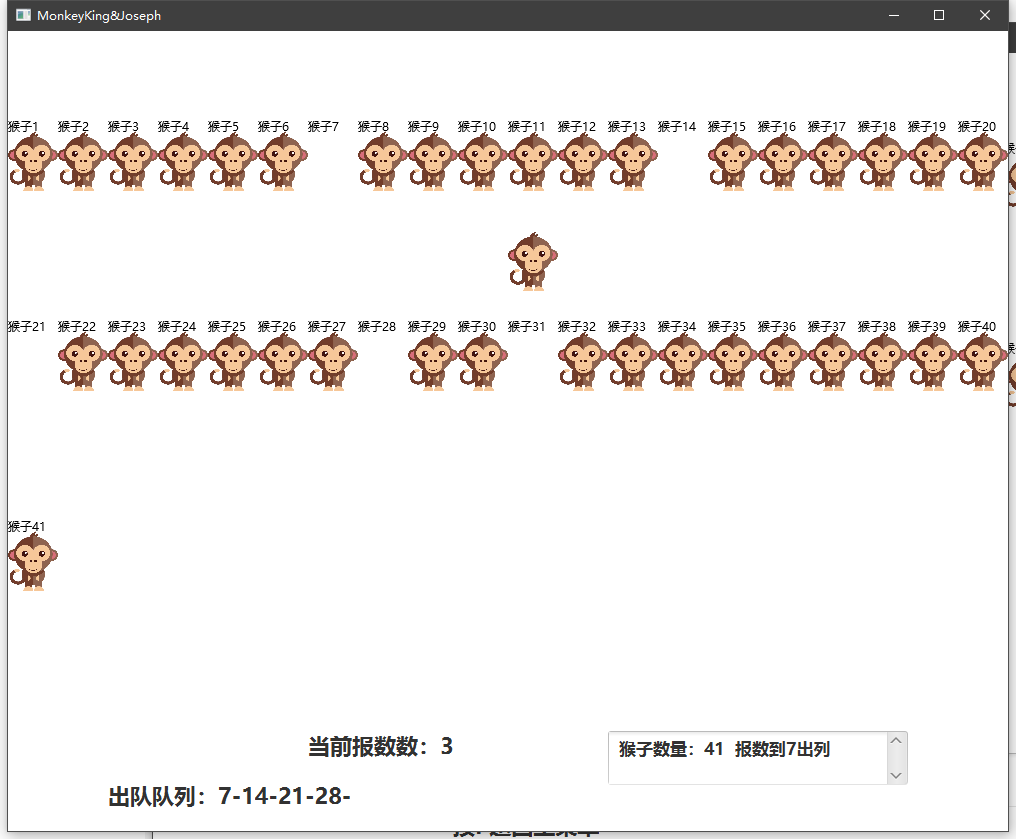
image-20220106063826976

joseph

image-20220106063914161

image-20220106063928978

课设总结

课程设计过程的收获

这次数据结构课设，让我了解了很多算法的设计，很多数据结构的使用。在设计迷宫时我学习编写使用了队列，双端队列，优先队列，栈，链表，数值和广义表。利用prim算法生成迷宫其实是一个最小生成树也就是传说的完美迷宫，而DFS设计的迷宫则是利用了栈的递归回溯。而迷宫节点设计其实是参考了广义表的设计。在写A星路径规划算法时，则是设计使用了优先队列，通过比较总代价（当前路径+绝对路径）来确定路径方向。在设计计算机项目时，则是使用了栈后进先出的特点，来求解逆波兰式计算算式结果。最后是猴子选大王项目和joseph项目，则是使用了队列的先进先出特点，设计的算法。

对数据结构这门课程的思考

学习数据结构之前、一直以为数据结构是一门新的语言、后来才知道学习数据结构是为了更加高效的的组织数据、设计出良好的算法，而算法则是一个程序的灵魂。经过了一学期的数据结构了，在期末之际对其进行总结。首先，学完数据结构我们应该知道数据结构讲的是什么，数据结构课程主要是研究非数值计算的研究的程序设计问题中所出现的计算机处理对象以及它们之间关系和操作的学科。