配套作业——递归算法
需求
编程实现斐波那契数列,分别用递归法,数组法。比较实验结果,分析原因。
设计空间复杂度更好的算法,实现斐波那契数列。
- 编程实现汉诺塔问题
- 全排列问题(选做)
实现
斐波那契数列
1 |
|
1 |
|
- fun1递归算法
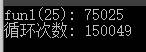
- fun2数组法
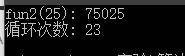
- 结论:数组法大大降低了时间复杂度,但利用了数组,提高了空间复杂度,典型的空间换取时间
- 因为我们在数组法中其实只要用到arr[n-1]和arr[n-2],所以我们可以迭代的方式来降低空间数组法的复杂,同时不提高时间复杂度
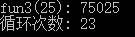
1 |
|
汉诺塔问题
1 |
|

全排列问题
1 |
|
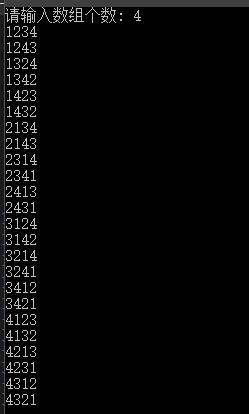
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Gallifrey的计算机学习日记!
评论


