找质数的优化算法

优化一

原理

2是唯一的偶数质数，先将2输出

其余的质数都是奇数，所有被除数从3开始算，每次加2，遍历所有范围内的奇数

除数从3开始遍历，遍历到被除数的平方（一个数因数都是一个大于等于该数平方，一个小于等于该数平方，成对出现）

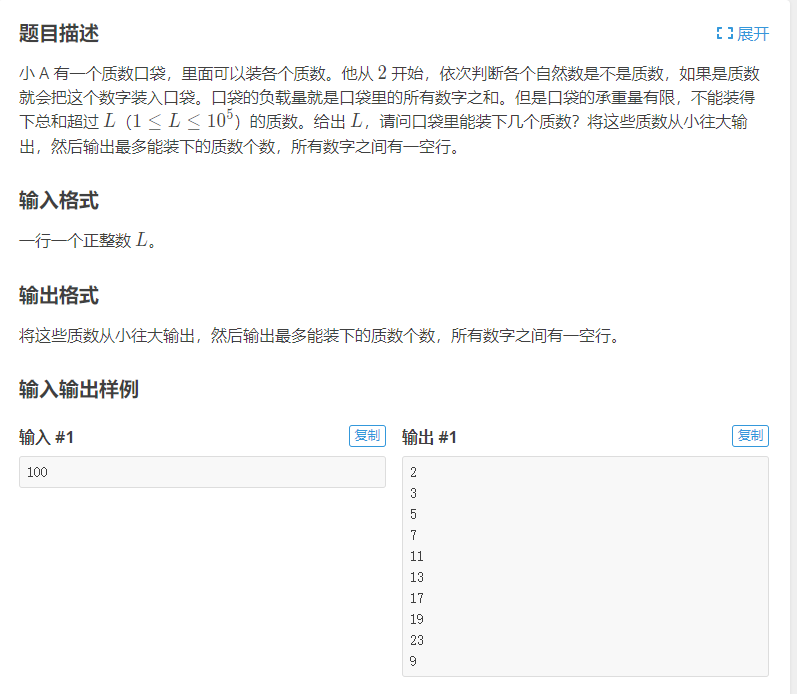
例题与代码

题目一

代码

#include <iostream>
#include <cmath>
using namespace std;

int main()
{
	int N ;
    cin >> N;
    if(N>=2){
	printf("2\n");// 2 是质数
    }    
	for (int i = 3; i < N; i += 2) {//质数除了2之外，其他都是奇数
		bool flag = true;//质数标记 一开始为true，有一个数能被整除则改成false
		int stop = sqrt(i);//因数是成对出现的，只有平方自己和平方前的数就可以了
		for (int j = 3; j <=stop; j += 2) {
			if (i % j == 0) { 
				flag = false;
				break;
			}
		}
	
		if (flag) printf("%d\n", i);
	}
	return 0;
}

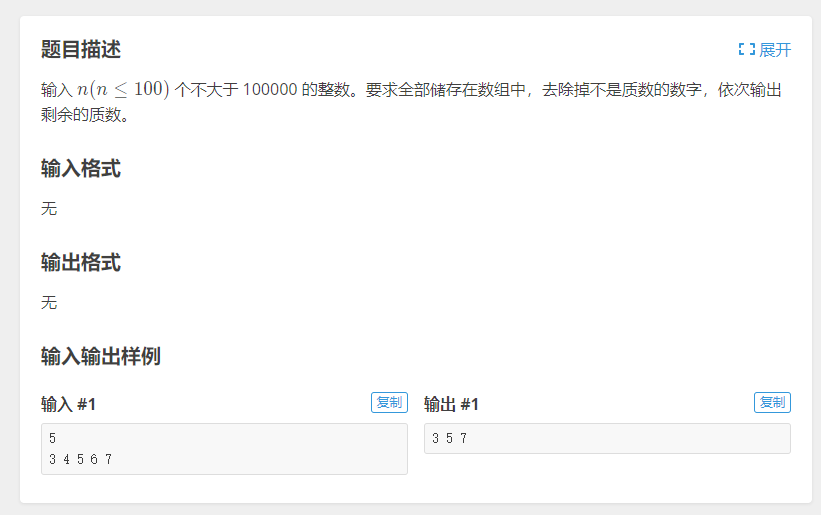
题目二

代码

#include <iostream>
using namespace std;

int N;
int arr[100];

int main() {
	cin >> N;
	int t = 0;
	while (t < N) {
		cin >> arr[t];
		t++;
	}
	

	for (int i = 0; i < N; i++) {
		bool flag = true;

		//判断1
		if (arr[i] == 1) flag = false;
		//判断是不是偶数 除了2，其他的偶数一定不是质数
		if (arr[i]!=2 && arr[i]%2 == 0)  flag = false;

		//判断9到正无穷的数 因为3 5 7是质数刚好直接输出 
		for (int j = 3; j <= sqrt(arr[i]); j+=2) {
			if (arr[i] % j == 0) {
				flag = false;
				break;
			}
		}
		if (flag) printf("%d ", arr[i]);
	}
	return 0;
}

优化二埃氏筛

原理

如果我们想要知道小于等于 n 有多少个素数呢？

一个自然的想法是我们对于小于等于 n 的每个数进行一次判定。这种暴力的做法显然不能达到最优复杂度，考虑如何优化。

考虑这样一件事情：如果 i 是合数，那么 i 的倍数也一定是合数。利用这个结论，我们可以避免很多次不必要的检测。

如果我们从小到大考虑每个数，然后同时把当前这个数的所有（比自己大的）倍数记为合数，那么运行结束的时候没有被标记的数就是素数了。

时间复杂度

$O(nlogn)$

代码

#include <iostream>

using namespace  std;
const long long  int N=100000000;
long long int is_prime[N];
long long int prime[N];
int Eratosthenes(long long int n) {
    long long int p = 0;

    //全假设为质数
    for (long long int i = 0; i <= n; ++i) is_prime[i] = 1;
    //0，1提前设为合数
    is_prime[0] = is_prime[1] = 0;


    for (long long int i = 2; i <= n; ++i) {
        if (is_prime[i]) {
            prime[p++] = i;  // prime记录质数
            // 因为从 2 到 i - 1 的倍数我们之前筛过了，这里直接从 i的倍数开始，提高了运行速度
            // 因为小于i*i的数,如果是合数，这个合数肯定有一个因数肯定小于是i的，在前面就被筛选掉了
            for (long long int j = i * i; j <= n;j += i)
                is_prime[j] = 0;  //是i的倍数的均不是素数 标记为掉
        }
    }
    return p;
}
int main(){
    long long int n;
    cin>>n;
    for(int i=0;i<Eratosthenes(n);i++) printf("%lld\n",prime[i]);


    return 0;
}

优化三欧拉筛

原理

在埃氏筛的基础上优化，每次只筛选到（i*（i除了1之外最小公因数的数）

确保不重复筛选

(加一行代码)

时间复杂度

$O(n)$

代码

#include <iostream>

using namespace  std;
const long long  int N=10000000;
long long int is_prime[N],prime[N];
int cnt=0;

void init(long long int MAXN) {

    for (long long int i = 2; i <= MAXN; i++) {
        if (!is_prime[i]) {
            prime[cnt++] = i;
        }
        for (long long int j = 0; j < cnt; j++) {
            if ( i * prime[j] > MAXN) break;
            is_prime[i * prime[j]] = 1;
            if(i%prime[j]==0)  break;//关键
        }
    }
}


int main(){
    long long int n;
    cin>>n;
    init(n);
    for(int i=0;i<cnt;i++) printf("%lld ",prime[i]);
    return 0;
}

1	if(i%prime[j]==0) break;//关键

参考文献：

找质数的优化算法

优化一

原理

例题与代码

题目一

代码

题目二

代码

优化二 埃氏筛

原理

时间复杂度

优化三 欧拉筛

原理

时间复杂度

代码

优化二埃氏筛

优化三欧拉筛