算法设计与应用——动态规划

动态规划简介

Dynamic Programming

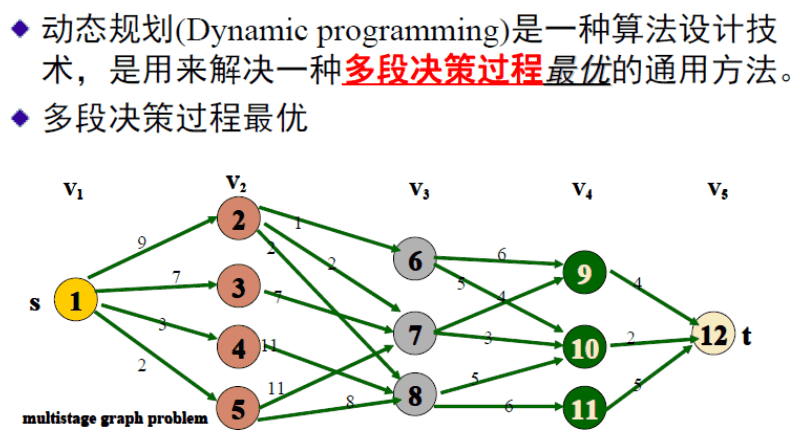
• 动态规划是求解某类问题的一种方法，是考察问题的一种途径，而不是一种算法。必须对具体问题进行具体分析，运用动态规划的原理和方法，建立相应的模型，然后再用动态规划方法去求解。

多阶段决策问题

• 是动态决策问题的一种特殊形式；

• 在多阶段决策过程中,系统的动态过程可以按照时间进程分为状态相互联系而又相互区别的各个阶段；

• 在多阶段决策过程中,系统的动态过程可以按照时间进程分为状态相互联系而又相互区别的各个阶段；

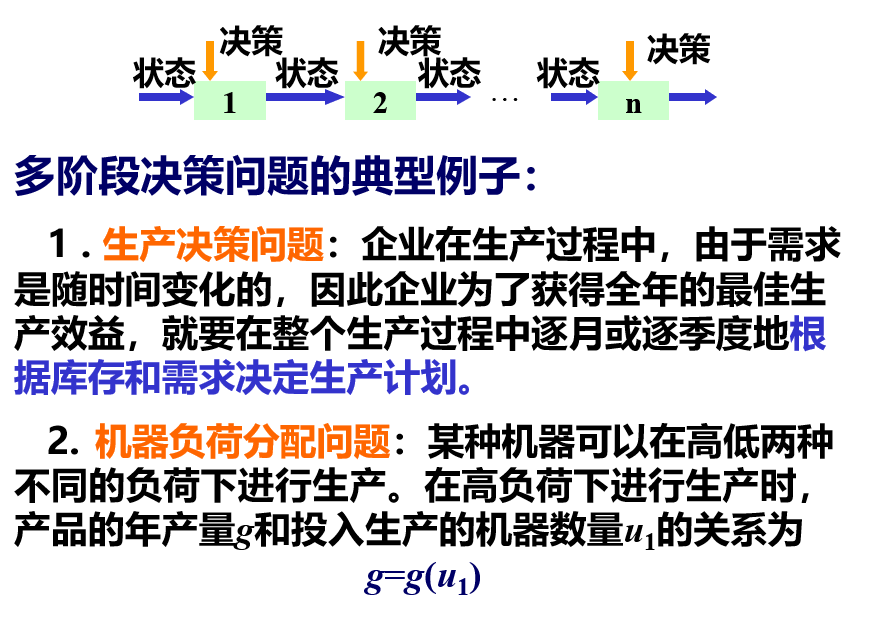
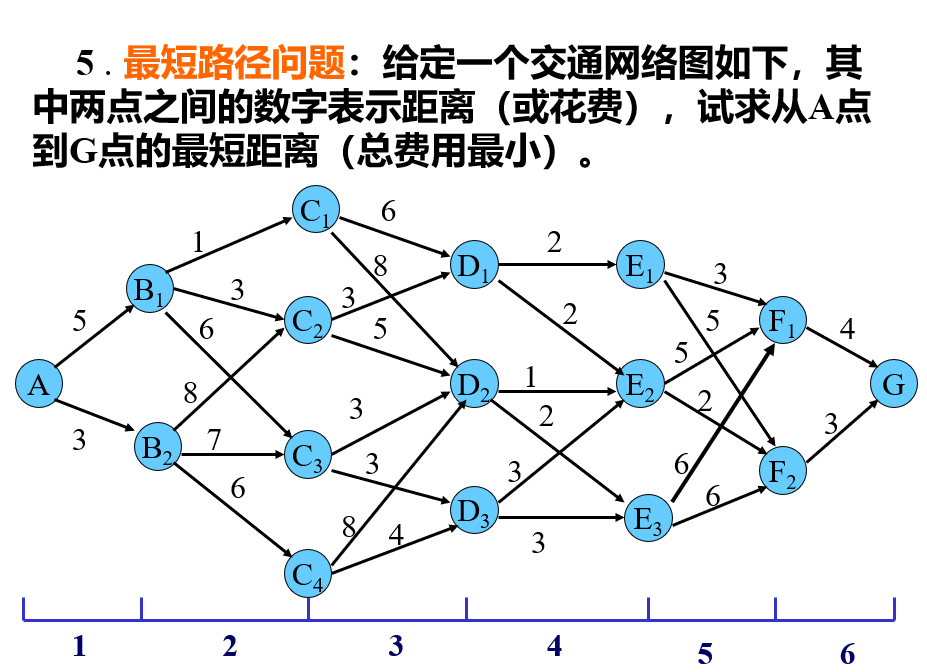
动态规划的基本思想

基本概念

• 阶段：

  • 把一个问题的过程，恰当地分为若干个相互联系的阶段，以便于按一定的次序去求解。
  • 描述阶段的变量称为阶段变量k 。

• 状态：

  • 表示每个阶段开始所处的条件。
  • 通常一个阶段有若干个状态，描述过程状态的变量称为状态变量s~k~ 。

• 决策：

  • 当处于某一阶段的某个状态时，可以作出不同的决定，从而确定下一阶段的状态，这种决定称为决策。
  • 描述决策的变量，称为决策变量uk。

• 多阶段决策过程

  • 其发展是通过一系列的状态转移来实现的；
  • 通常，系统在某一阶段的状态转移不但与系统的当前的状态和决策有关，而且还与系统过去的历史状态和决策有关。

• 策略

  • 是一个按顺序排列的决策组成的集合。
  • 从允许策略集合中找出达到最优效果的策略称为最优策略。

动态规划问题的特征

最优子结构

• 无论过去的状态和决策如何，相对于前面的决策所形成的状态而言，余下的决策序列必然构成最优子策略。”也就是说，一个最优策略的子策略也是最优的.也称最优化原理。

• “整体最优则局部最优。”反之不一定成立

重叠子问题：

• 在用递归算法自顶向下解问题时，每次产生的子问题并不总是新问题，有些子问题被反复计算多次。
• 动态规划算法正是利用了这种子问题的重叠性质，对每一个子问题只解一次，而后将其解保存在一个表格中，在以后尽可能多地利用这些子问题的解。

无后效性原则

马尔可夫性

• 如果某阶段状态给定后，则在这个阶段以后过程的发展不受这个阶段以前各段状态的影响；
• 过程的过去历史只能通过当前的状态去影响它未来的发展；
• ​ 状态具有无后效性的多阶段决策过程的状态转移方程如下

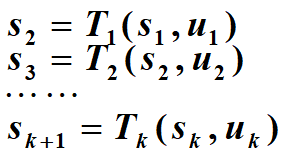
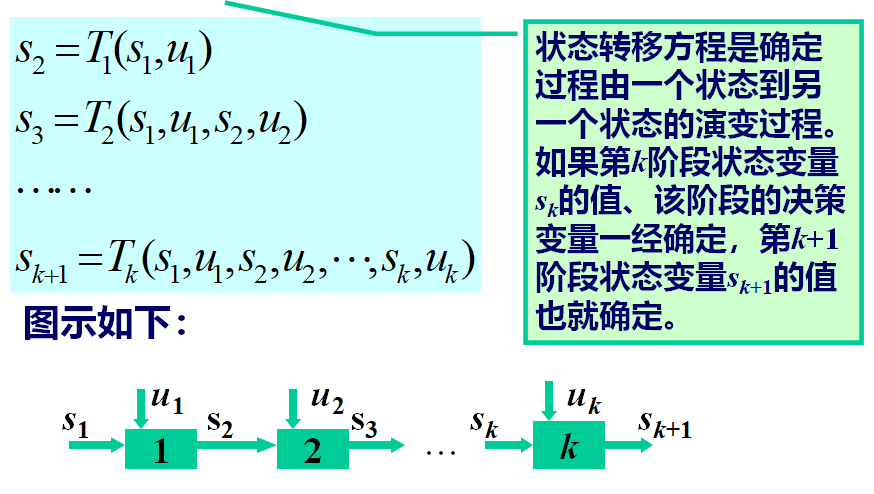
能用动态规划方法求解的多阶段决策过程是一类特殊的多阶段决策过程，即具有无后效性的多阶段决策过程。

01背包问题

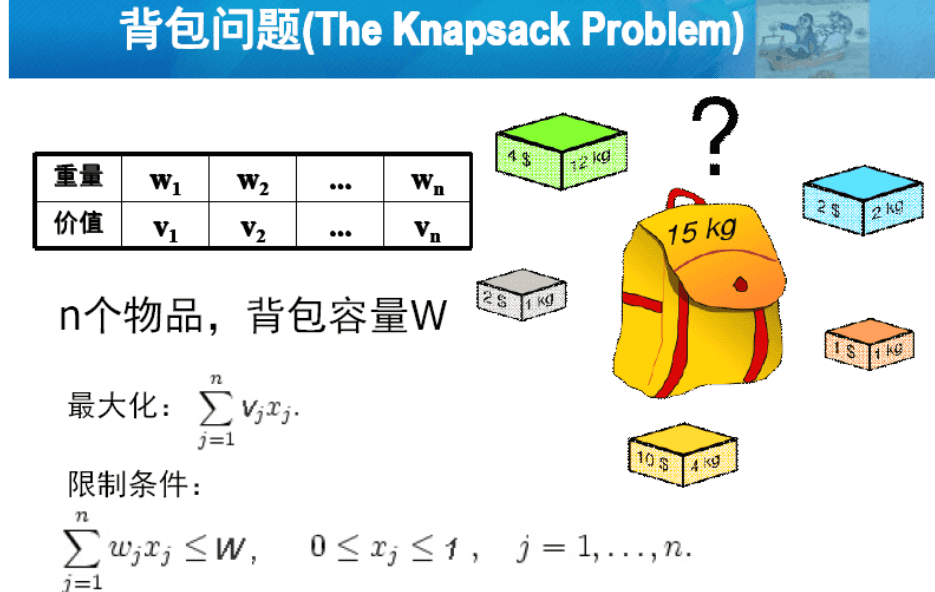
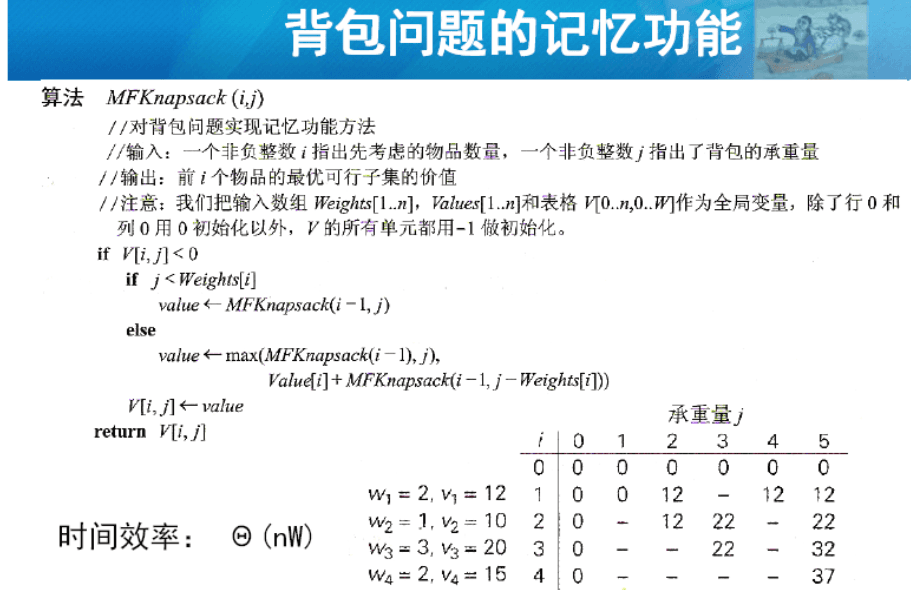
配套作业

配套作业——动态规划

https://gallifrey.asia/posts/243a1ddab2db/