算法设计与应用——贪心策略
贪心策略基本思想
换硬币问题

贪心算法思想

适用问题

活动安排问题

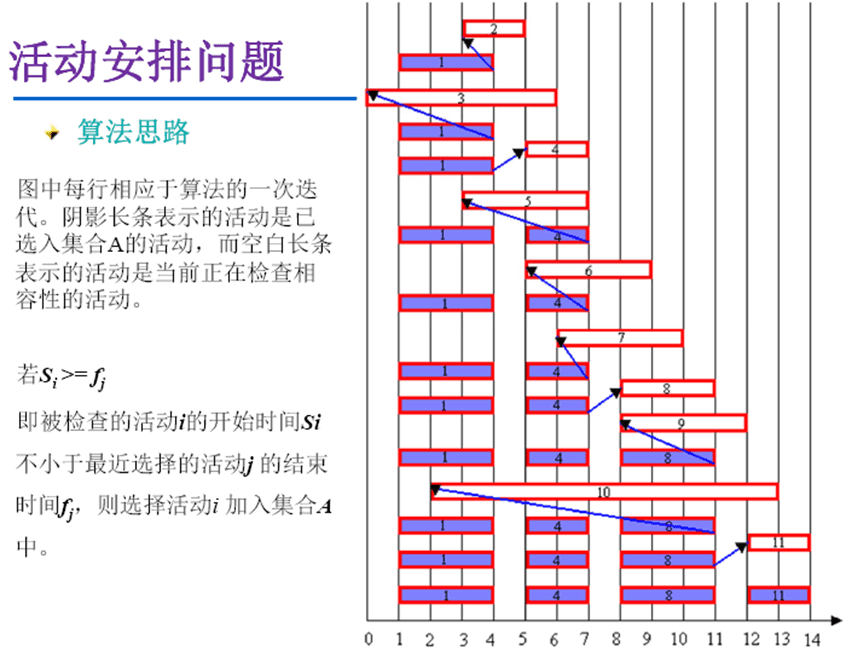
算法实现
- 这里是代码是不完整的,执行前,编写并执行先一个排序


贪心的基本要素



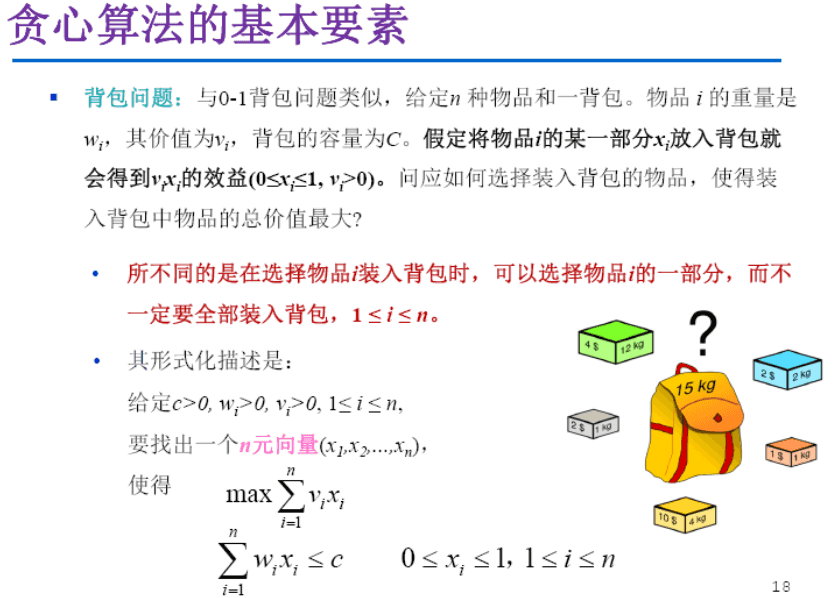






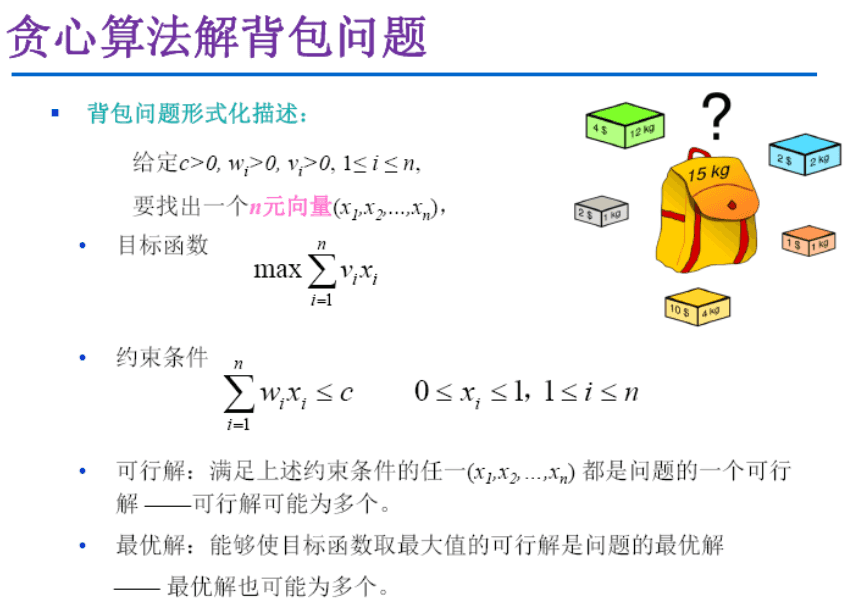
背包问题
- 注意:这里是普通背包问题,不是01背包问题
贪心依据的选择

价值优先——次优解



容量优先——次优解


单位利益值——最优解


算法实现


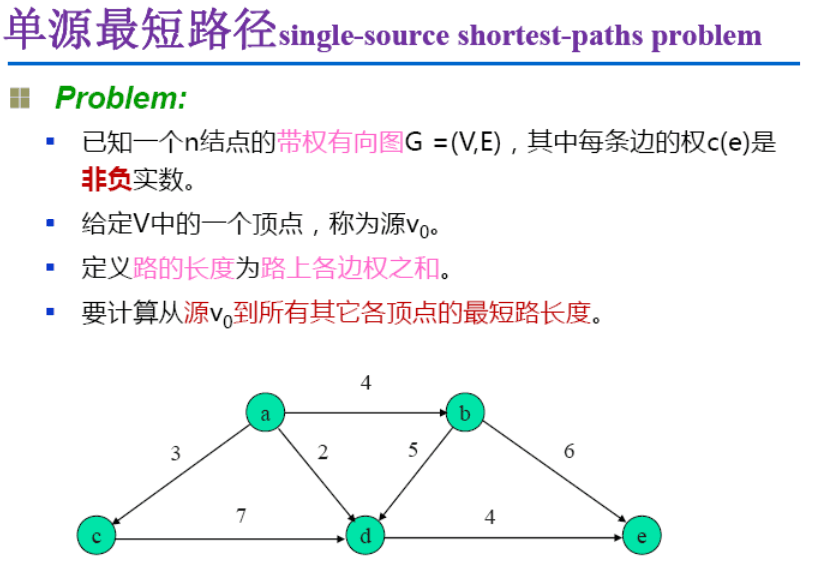
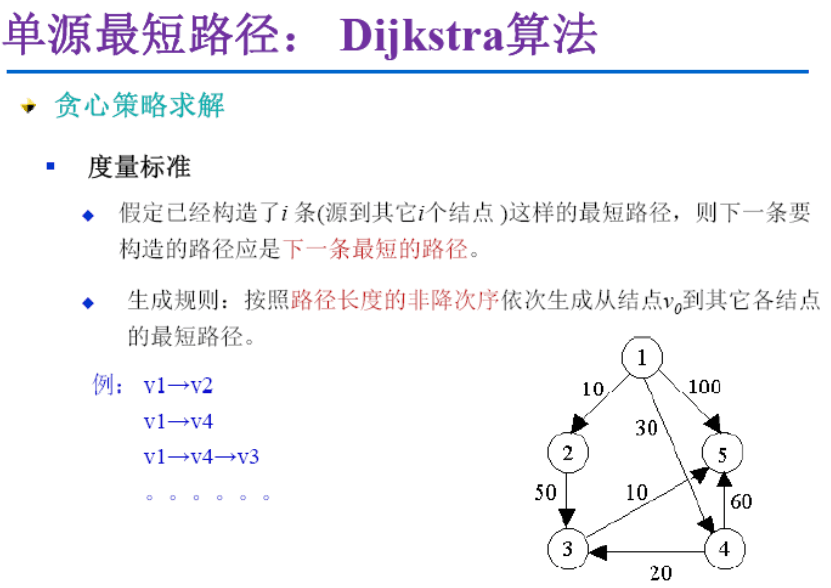
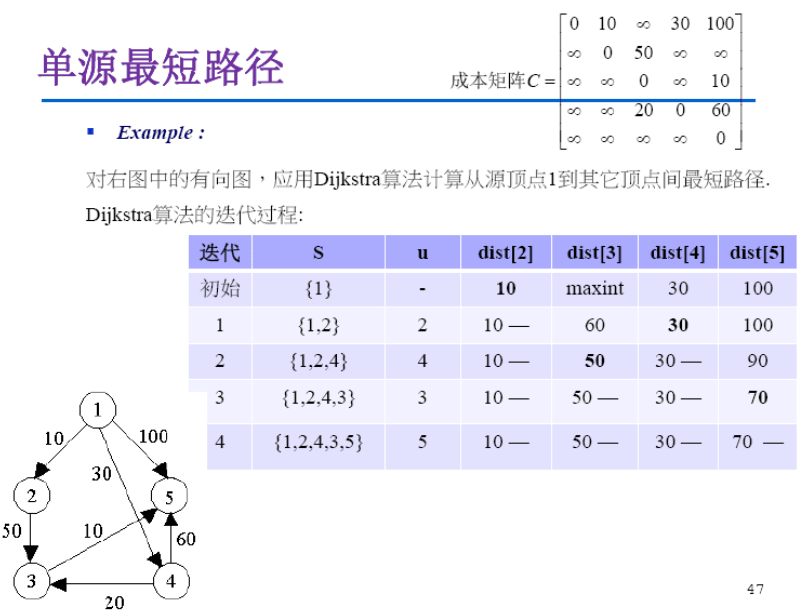
Dijkstra算法


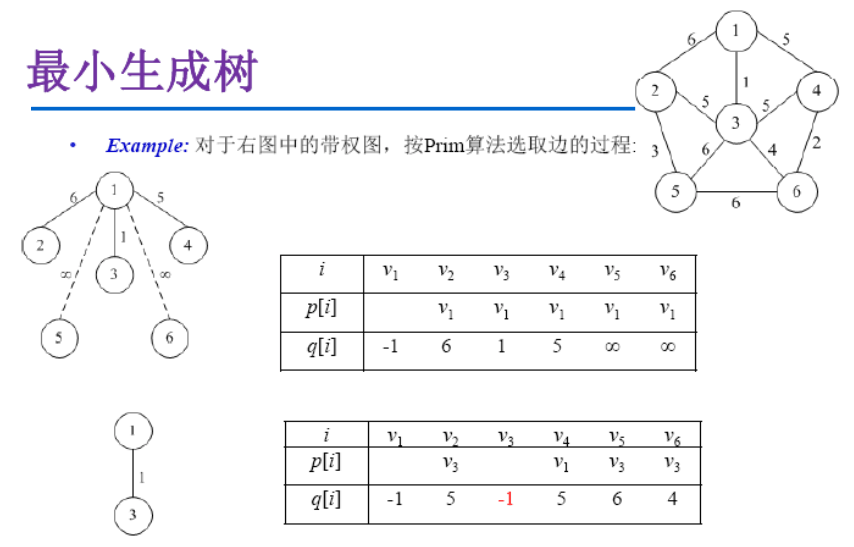
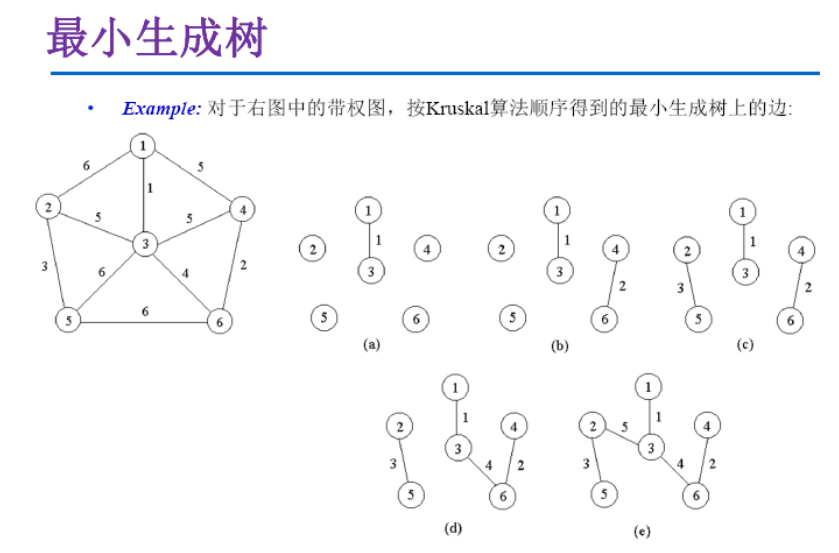
最小生成树


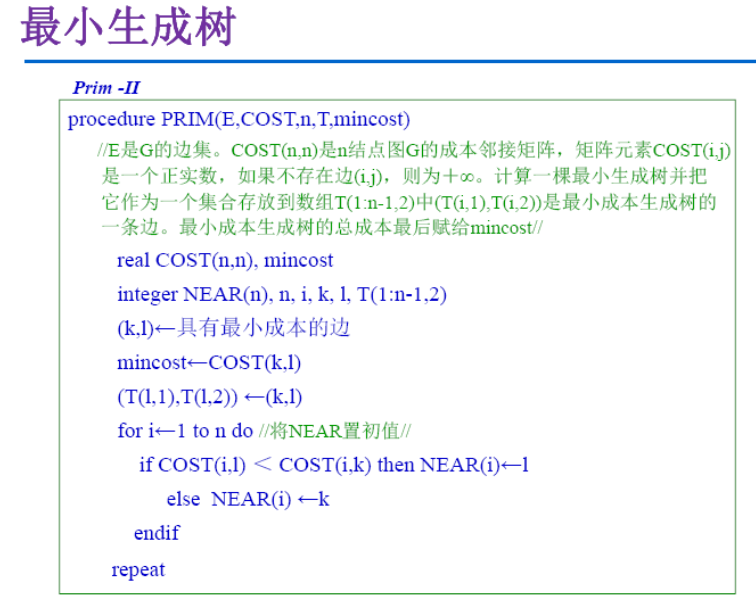
Prim算法



Kruskal算法
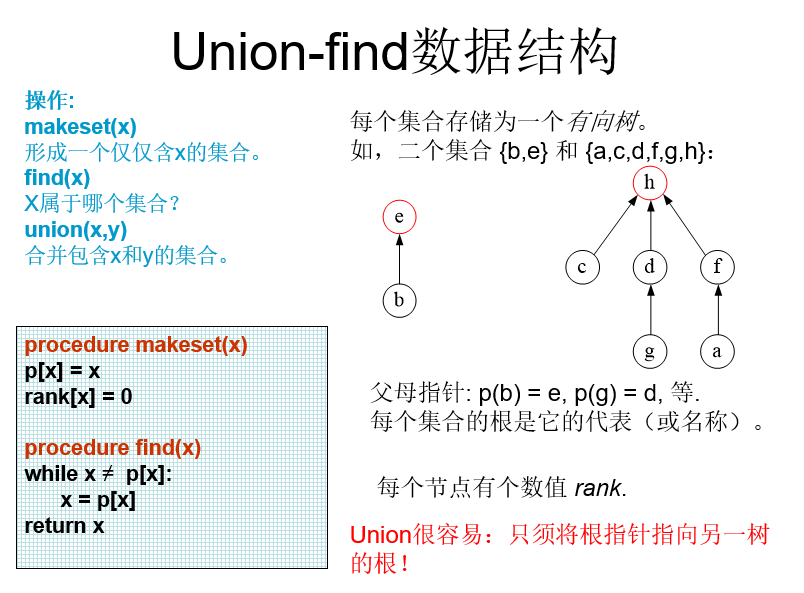
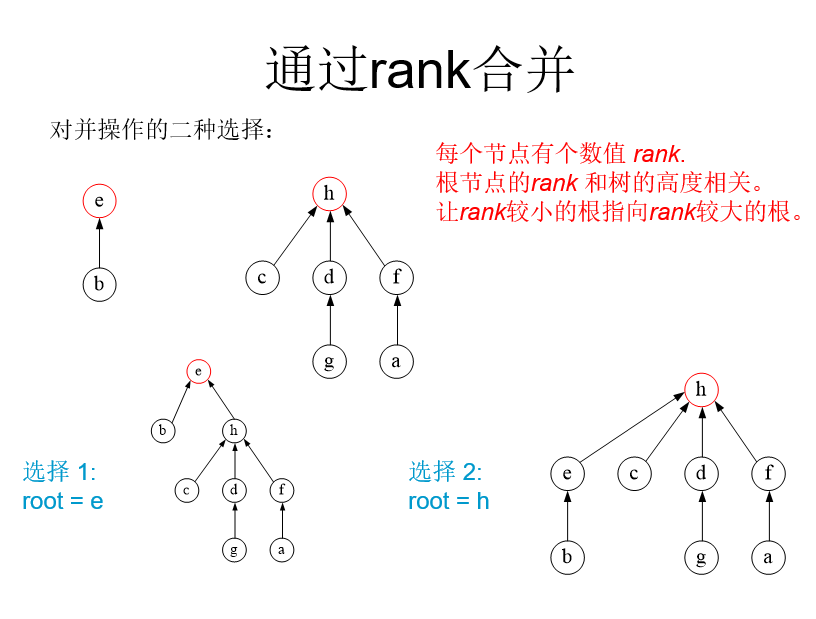
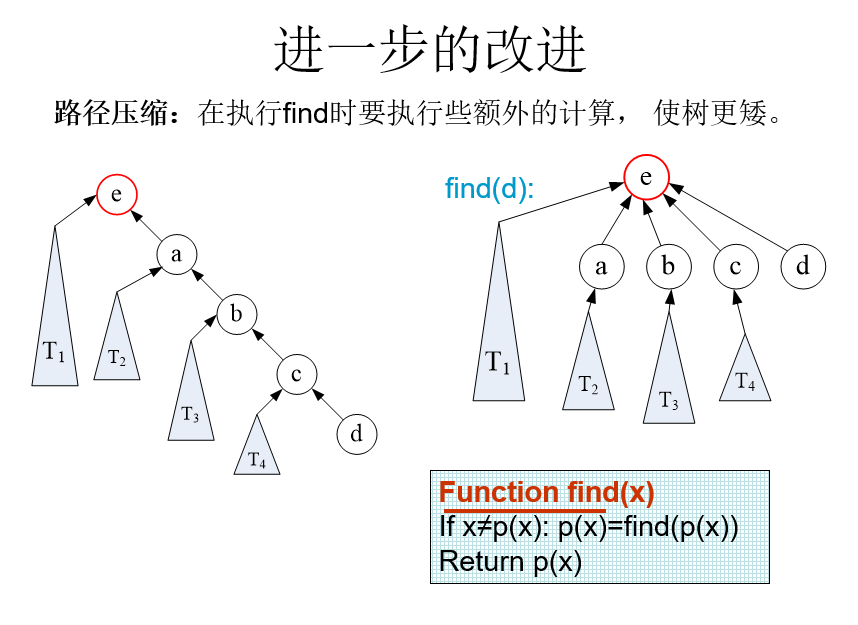
解决环的问题




哈夫曼编码
- Data Compression via Huffman Coding
- Motivation
- Limited network bandwidth.
- Limited disk space.
- Human codes are used for data compression.
- Reducing time to transmit large files, and
- Reducing the space required to store them on disk or tape.
- Huffman codes are a widely used and very effective technique for compressing data, savings of 20% to 90% are typical, depending on the characteristics of the data.
- Motivation
问题提出
- Problem
- Suppose that you have a file of 100K characters. To keep the example simple, suppose that each character is one of the 6 letters from a through f. Since we have just 6 characters, we need just 3 bits to represent a character, so the file requires 300K bits to store. Can we do better?
- Suppose that we have more information about the file:
- the frequency which each character appears
- Solution
- The idea is that we will use a variable length code instead of a fixed length code (3 bits for each character), with fewer bits to store the common characters, and more bits to store the rare characters
Example of Data Compression数据压缩示例
- For example, suppose that the characters appear with the following frequencies, and following codes:
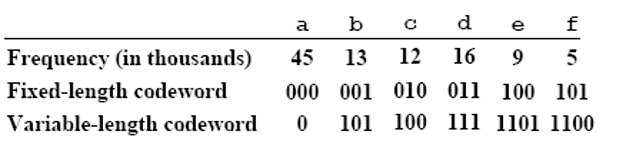
- Then the variable-length coded version will take not 300K bits but 451 + 133 + 123 + 163 + 94 + 54 = 224K bits to store, a 25% saving. In fact this is the optimal way to encode the 6 characters present, as we shall see
Characteristic of Optimal Code
Represented as a binary tree whose leaves are the given characters
In an optimal code each non-leaf node has two children
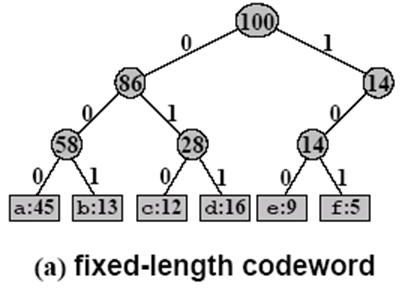
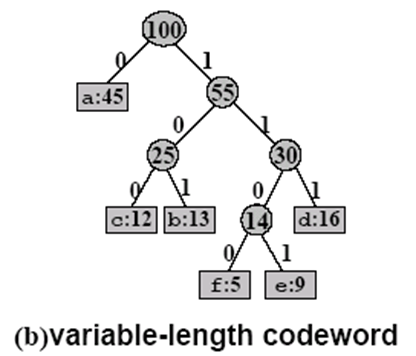
Prefix-free Code((非)前缀编码)
In a Prefix code no codeword is a prefix of another code word没有一个编码是另一个编码的前缀
- Easy encoding and decoding
To encode, we need only concatenate the codes of consecutive characters in the message
- The string 110001001101 parses uniquely as 1100-0-100-1101, which decodes to FACE
To decode, we have to decide where each code begins and ends
Easy, since, no codes share a prefix
“prefix-free codes” would be a better name, but the term “prefix codes” is standard in the literature
Algorithm of Huffman Coding
- The greedy algorithm for computing the optimal Human coding tree T is as follows
- It starts with a forest of one-node trees representing each c ∈*C, and merges them in a greedy style, using a priority queue Q*, sorted by the smallest frequency:

配套作业
本博客所有文章除特别声明外,均采用 CC BY-NC-SA 4.0 许可协议。转载请注明来自 Gallifrey的计算机学习日记!
评论



