算法设计与应用——算法基础
斐波那契问题
假设兔子出生一个月后能繁殖,以后每月产一个孩子,一直下去直到永远。从一个兔子开始,问n个月后有多少个兔子?
递归算法求解
1 | function Fib1(n) |
计算 F200 大概需要 2140 个运算.
在一个快速计算机上要花多长时间?(在NEC Earth Simulator上花2^92秒)
- 指数爆炸,所以算法很重要
算法的基础概念
算法的特征
- 输入性:有零个或多个外部量作为算法的输入。
- 输出性:算法产生至少一个量作为输出。
- 确定性:组成算法的每条指令清晰、无歧义。
- 有穷性:算法中每条指令的执行次数有限,执行每条指令的时间也有限。
- 可行性: 算法原则上能够精确地运行,而且人们用笔和纸做有限次运算后即可完成。
程序是算法用某种程序设计语言的具体实现。
程序可以不满足算法的性质(4)即有穷性。
如操作系统
算法的4个标准
- 正确性:在合理的数据输入下,能在有限的时间内得出正确的结果。
- 可读性:应易于人的理解,易于调试。
- 健壮性:具备检查错误和对错误进行适当处理的能力。
- 效率:算法执行时所需计算机资源的多少,包括运行时间和存储空间。
算法的描述形式
自然语言
- 优点:容易理解
- 缺点:冗长、不够严谨、二义性
- 使用方法:粗线条描述算法思想
- 注意事项:避免写成自然段
算法框图法
- 优点:流程图、盒图,流程直观、简洁、明了,便于理解和交流
- 缺点:缺少严密性、灵活性
- 使用方法:描述简单算法
- 注意事项:注意抽象层次
- 例:欧几里得算法
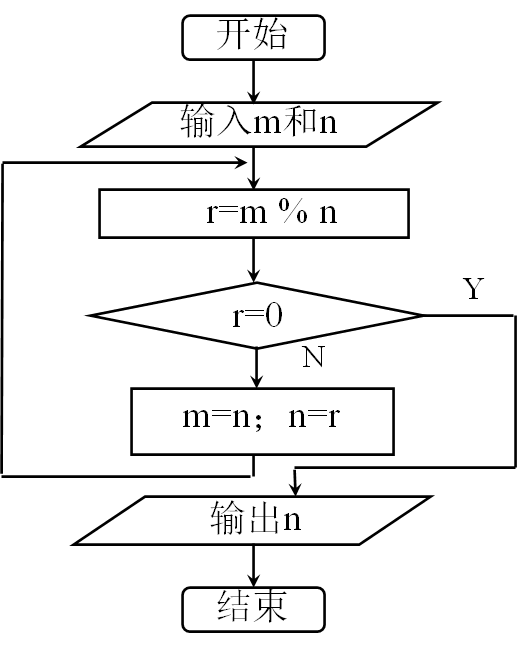
伪代码语言描述法
伪代码(Pseudocode):介于自然语言和程序设计语言之间的方法,它采用某一程序设计语言的基本语法,操作指令可以结合自然语言来设计。 (算法语言)
优点:表达能力强,抽象性强,容易理解
例子:欧几里得算法
1
2
3
4
5
61. r = m % n;
2. 循环直到 r 等于0
2.1 m = n;
2.2 n = r;
2.3 r = m % n;
3. 输出 n ;
高级程序设计语言描述法
- 优点:能由计算机执行
- 缺点:抽象性差,对语言要求高
- 使用方法:算法需要验证
- 注意事项:将算法写成子函数
1 |
|
算法设计的一般过程
- 充分理解要解决的问题
- 数学模型拟制
- 算法详细设计
- 算法描述
- 算法思路的正确性验证
- 算法分析
- 算法的计算机实现和测试
- 文档资料的编制
著名公式
Algorithm + Data Structure = Programming
算法分析
- 算法复杂性 = 算法运行时所需要的计算机资源的量
- 时间复杂性、空间复杂性
- 影响时间复杂性的因素(查找为例)
- 问题规模n、输入序列I、算法本身A
- 影响空间复杂性的因素
- 算法本身、输入输出数据、辅助变量
- 算法复杂性的权衡
- 时间复杂度和空间复杂度相互影响(时间换空间或空间换时间)
三种情况下的复杂性(结合查找操作)
- 最好情况Tmin(N)
- 1次
- 最坏情况Tmax(N)
- N次
- 平均情况Tavg(N)
- (N+1)/2
算法渐近复杂性态
- 设算法的运行时间为T(n),如果存在T*(n),使得
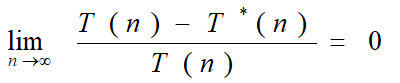
就称T*(n)为算法的渐进性态或渐进时间复杂性。
举例说明:
假设算法A的运行时间表达式为T1(n)
T1(n)=30n4+20n3+40n2+46n+100
假设算法B的运行时间表达式为T2(n)
T2(n)=1000n3+50n2+78n+10
随着n的增大,对算法的执行时间影响最大的是最高次方。
算法A的运行时间可记为:T1(n)≈n4
算法B的运行时间可记为:T2(n)≈n3
渐近符号
O—上界
W—-下界
Q—-上界和下界
算法分析中常见的复杂性函数
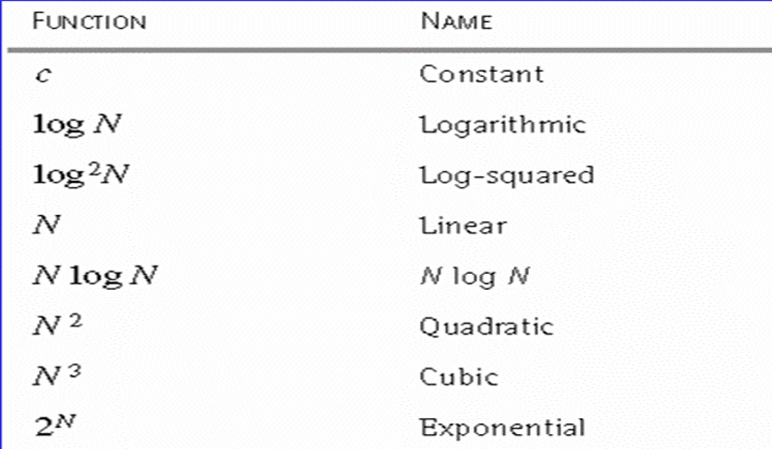
几种常见的时间复杂度函数按数量级从小到大的顺序依次是:
- Θ(lgn),Θ(sqrt(n)),Θ(n),Θ(nlgn),Θ(n^2^),Θ(n^3^),Θ(2^n^),Θ(n!)
在多项式中,n的最高次指数是最主要的决定因素,常数项、低次幂项和系数都是次要的。
时间复杂度分析的基本规则
- 主要考虑可执行语句的情况:
- 输入、输出、赋值语句,为O(1);
- 顺序结构,采用渐进式O的求和规则来进行计算;
- 选择结构,考虑判定后所执行语句的执行时间
- O(max(T(s1), T(s2)));
- 循环结构,考虑循环判定条件和循环体语句的执行时间,采用渐进式O的乘积规则来进行计算;
- 复杂算法,先分割,然后采用渐进式O的求和规则和乘法规则来计算整个算法的时间复杂度;
空间复杂度
- 算法所占用的存储空间包括
- 算法自身
- 输入、输出
- 辅助空间
- 空间复杂度S(n)=O(f(n)),以最坏情况来分析
递归
什么是递归
子程序(或函数)直接调用自己或通过一系列调用语句间接调用自已,称为递归。直接或间接调用自身的算法称为递归算法 。
采用递归算法来求解问题的一般步骤:
分析问题,寻找递归关系
找出停止条件
- 构建函数体
n的阶乘

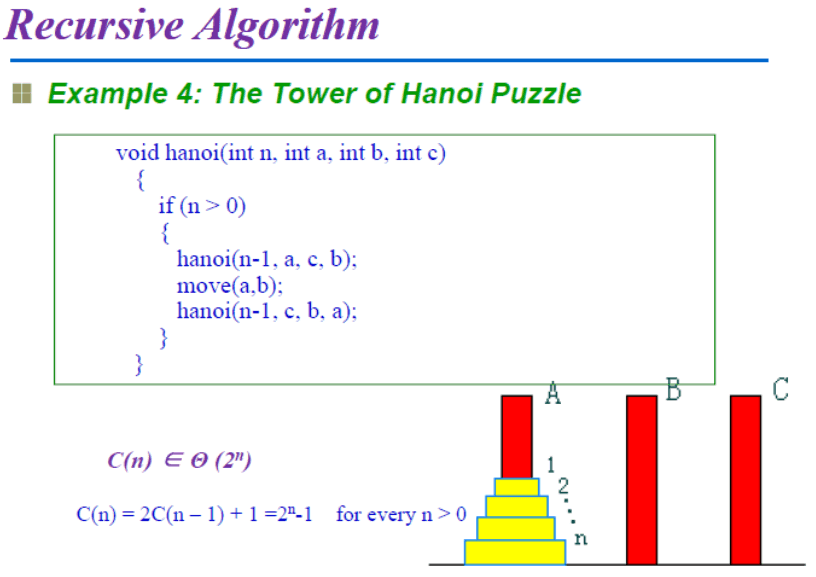
汉诺塔问题
- 分解一下递归
- 先把A柱子上面的n-1个盘子从A柱移动到C柱
- 然后A柱最下面的盘中就可以从A移动B柱了
- 最后C柱上n-1个盘中移动到B柱
全排列问题


递归算法的两种类型

再看斐波那契问题
- Fibonacci数列一个较好的算法,用一个数组储存每次计算的数值,类似记忆搜索
1 | function Fib2(n) |
- 和原来的递归算法时间复杂度比较
1 | function Fib1(n) |
Fib1: O(n 2^0.7n^ ) 时间 仍然是个大的突破:
Fib2: O(n^2^ 时间 从指数级到多项式级



