配套作业——搜索

需求

• 百钱白鸡问题，穷举法求解，要求二重循环编程解决。
• DFS算法编程实现
• 0-1背包问题，回溯法编程解决（剪枝函数选做，非必需）

• 8皇后问题，回溯法编程实现

• BFS算法编程实现

实现

百钱百鸡问题

• 代码实现
• 测试运行

#include<iostream>
using namespace std;

int main() {
	int a, b;
	for (a = 1; a <= 20; a++)
		for (b = 1; b <= 33; b++) {
			if ((100 - a - b) % 3 == 0&&(5 * a + 3 * b + (100 - a - b) / 3 == 100)) {
				printf("%d %d %d\n", a, b, 100-a-b);
			}
		}
}

DFS实现

• 代码实现
• 测试运行

• 这里是利用DFS实现图的遍历，测试图如下

  

public class DFS {
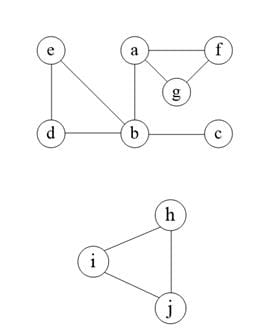
    char[] vertex={'a','b','c','d','e','f','g','h','i','j'}; //顶点名称
    int n=10;//顶点数量
    int []visited=new int[n];//是否访问
    //邻接矩阵图
    int edge[][]={
        //  a  b c d e f g h i j
            {0,1,0,0,0,1,1,0,0,0},      //a
            {1,0,1,1,1,0,0,0,0,0},      //b
            {0,1,0,0,0,0,0,0,0,0},      //c
            {0,1,0,0,1,0,0,0,0,0},      //d
            {0,1,0,1,0,0,0,0,0,0},      //e
            {1,0,0,0,0,0,1,0,0,0},      //f
            {1,0,0,0,0,1,0,0,0,0},      //g
            {0,0,0,0,0,0,0,0,1,1},      //h
            {0,0,0,0,0,0,0,1,0,1},      //i
            {0,0,0,0,0,0,0,1,1,0},      //j
    };

    //初始化
    void init(){
        for (int i=0;i<=n-1;i++)   // n个顶点标志位初始化
        visited[i]=0;
    }

    //对图g的顶点K进行深度遍历
    void DFSk (Graph g, int k)
    {  visited[k]=1;
        // visit k 访问k顶点，我们把k的名字输出一下
        System.out.print(vertex[k]+"已访问  ");
        for (int i=0;i<=n-1;i++)
        if (g.edge[k][i]==1 && visited[i]==0)  DFSk(g,i);
    }

    //考虑g的连通性
    void DFSt (Graph g) {
        for (int i=0;i<=n-1;i++) {
            if (visited[i] == 0){
                System.out.print("\n本次访问头："+vertex[i]+"  ");//输出一下访问头，非连通则换行
                DFSk(g, i);
            }
        }
    }


    public static void main(String[] args) {
        System.out.println("访问顺序：");
        DFS dfs=new DFS();
        dfs.DFSt(new Graph(dfs.vertex, dfs.edge));
    }

}

//邻接矩阵表示图
class Graph {
    char []vertex;//顶点信息
    int edge[][];//边信息

    public Graph(char[] vertex, int[][] edge) {
        this.vertex = vertex;
        this.edge = edge;
    }
}

回溯法解决01背包问题

• 代码实现
• 测试运行
• 剪枝优化

#include <iostream>
using namespace std;

const int N = 100000;

double currentWeight;	//当前重量	
double maxWeight;		//最大重量
double currentValue;	//当前价值
double bestValue;		//最大价值
int n;					//物品数量
double value[N];		//用一个数组记录每个物品的价值
double weight[N];		//用一个数组记录每个物品的重量
int bestRes [N];		//用一个数组记录最好结果的序号
int x[N];				//回溯作为容器记录物品01状态的数组

void backtrack(int t) {
	
	if (t > n) {//已遍历全部物体,得到一组解
		//判断是否更新最优解
		if (currentValue > bestValue) {
			bestValue = currentValue;
			for (int i = 0; i < n; i++) bestRes[i] = x[i];
		}
	}
	else {
		for (int i = 0; i <= 1; i++) {
			//设置物品状态 1要 0不要 所以说是01背包问题
			x[t] = i;
			//1的话,不超重则进入下一个物品的判断
			if (x[t]==1&& (currentWeight + weight[t] < maxWeight)) {
				currentValue += value[t];		//更新当前价值
				currentWeight += weight[t];		//更新当前重量
				backtrack(t + 1);
				currentValue -= value[t];		//回退价值
				currentWeight -= weight[t];		//回退重量
			}
			//0则直接进入下一个物品判断
			if (x[t] == 0) {
				backtrack(t + 1);
			}
		}
	}
}

int main() {

	cout << "输入背包最大容量maxWeight，物品数目n" << endl;
	cin >> maxWeight>> n;
	cout << "输入n件物品的重量weight与价值value" << endl;
	for (int i = 0; i < n; i++) {
		cin >> weight[i] >> value[i];
	}
	
	backtrack(0);//子集树回溯
	cout << "最大价值为" << bestValue << endl;
	cout << "放入背包的物品序号" << endl;

	for (int i = 0; i < n; i++) {
		if (bestRes[i] ==1 ) {
			cout << i+1 << " ";
		}
	}
	return 0;

}

• 其实在直接回溯的过程中，我们有很多节点是没有必要去访问的，在这里我们可以设计剪枝函数去优化代码

• 文章参考(18条消息) 0 1背包回溯法详解_羊书change的博客-CSDN博客_01背包回溯

#include <iostream>
#include <algorithm>
using namespace std;
const int MAXN = 200;
int C, n;
int x[MAXN], bestK[MAXN];//存储节点序号
int cw;//cw存储当前已放入背包的重量
double bestv = -1, curv = 0;//bestv存储全局最大价值，curv存储当前的价值
struct Knap {
	int num;//物品的序号
	double weight;//必须是double才可以进行除法的比大小
	double value;//物品的价值
};
Knap K[MAXN];
bool Compare(Knap a, Knap b) {//单位重量价值高的排在前面
	return a.value / a.weight > b.value / b.weight;
}
double remainMaxValue(int k) {//求出不选择第k性价比物品时，有可能的剩余最大价值
	int rw = C - cw;//背包剩余的质量
	double b = curv;//当前已有的价值
	while (k + 1 <= n && K[k + 1].weight <= rw) {//如果还有物品，并且这个物品小于剩余的质量，则放入
		b += K[k + 1].value;//更新价值
		rw += K[k + 1].weight;//跟新剩余容量
		k = k + 1;//对下一个物品进行判断
	}
	if (k + 1 <= n) {//剩余的容量选择部分物品
		b = b + K[k + 1].value / K[k + 1].weight * rw;
	}
	return b;
}
void Backtrack(int k) {//对第k性价比的物品进行搜索
	if (k > n) {//所有的物品都循环完了
		if (curv > bestv) {
			bestv = curv;//记录最大值
			for (int i = 1; i <= n; ++i) {
				bestK[i] = x[i];//更新放入的物品序号
			}
		}
	}
	else {
		if (cw + K[k].weight <= C) {//如果当前这个序号的物品不超重(小于等于)，试着放入
			x[K[k].num] = 1;//把当前序号标记
			cw += K[k].weight;//更新当前重量
			curv += K[k].value;//更新当前价值
			Backtrack(k + 1);//进入下一步
			cw -= K[k].weight;//回退重量
			curv -= K[k].value;//回退价值
		}
		if (remainMaxValue(k) > bestv) {
			//如果不选择第k性价比的物品时剩余最大价值可以超过当前最大价值，有进行下一步的必要
			x[K[k].num] = 0;//不选择k
			Backtrack(k + 1);//下一步
		}
	}

}
int main() {
	cout << "输入背包容量C，物品数目n" << endl;
	cin >> C >> n;
	cout << "输入n件物品的重量与价值" << endl;
	for (int i = 1; i <= n; ++i) {
		K[i].num = i;
		cin >> K[i].weight >> K[i].value;
	}
	sort(K + 1, K + n + 1, Compare);//按照性价比进行排序
	Backtrack(1);//子集树回溯
	cout << "最大价值为" << bestv << endl;
	cout << "放入背包的物品序号" << endl;
	for (int i = 1; i <= n; ++i) {
		if (bestK[i] != 0) {
			cout << i << " ";
		}
	}
	return 0;
}

BFS实现

• 代码实现
• 测试运行

• 本来想写bfs实现图的遍历的，但是临近考试，时间有点紧，这个给大家展示一个我自己写的迷宫小游戏里面bfs解决迷宫问题的算法，也是算bfs的实现了

package com.gallifrey.mazegame4;



import javafx.animation.SequentialTransition;
import javafx.animation.TranslateTransition;
import javafx.scene.Group;
import javafx.scene.paint.Color;
import javafx.scene.shape.Polyline;
import javafx.scene.shape.Rectangle;
import javafx.util.Duration;

import java.util.Date;
import java.util.LinkedList;
import java.util.Queue;
import java.util.concurrent.LinkedBlockingQueue;

public class BFS implements SF{

    private LinkedList<Node> linkedList;
    private LinkedList<Node> linkedList2;
    private int front=-1;
    private int rear=-1;
    private Node[][] nodeMap;
    private MainMap mainMap;

    public BFS(MainMap mainMap) {
        this.mainMap = mainMap;
    }



    //查找
    public boolean find(){
        Node start= mainMap.getStart();
        Node end=mainMap.getEnd();
        start.setPre(-1);
        nodeMap =mainMap.nodeMap;

        linkedList=new LinkedList<>();
        Node temp=null;
        linkedList.offer(start);
        rear++;
        nodeMap[start.getX()][start.getY()].setValue(-1);
        while(!(front==rear)) {
            temp=linkedList.get(++front);
            //判断是不是终点
            if (temp.getX() ==end.getX() && temp.getY() ==end.getY()) {
                return true;
            }
            //遍历4个方向

            Node temp2 = null;
            for (int i = 0; i < 4; i++) {
                switch (i) {
                    case 0:
                        temp2 = new Node(temp.x, temp.y - 1);
                        break;
                    case 1:
                        temp2 = new Node(temp.x, temp.y + 1);
                        break;
                    case 2:
                        temp2 =  new Node(temp.x - 1, temp.y);
                        break;
                    case 3:
                        temp2 = new Node(temp.x + 1, temp.y);
                        break;
                }
                //可走进队
                if (temp2.getX()<mainMap.getCol()&&temp2.getX()>0&&temp.getY()>0&&temp2.getY()<mainMap.getRow()&&nodeMap[temp2.getX()][temp2.getY()].getValue()==0) {

                    linkedList.offer(temp2);
                    rear++;
                    temp2.id=linkedList.indexOf(temp2);
                    temp2.setPre(temp.getId());
                    nodeMap[temp2.getX()][temp2.getY()].setValue(-1);
                }
            }
        }

        return false;
    }

    public  boolean find2(){
        linkedList2=new LinkedList<>();
        linkedList2.add(linkedList.get(front));
        int j=0;
        while (linkedList2.get(j).getPre()!=-1){
            linkedList2.add(linkedList.get(linkedList2.get(j).getPre()));
            j++;
        }
        linkedList=linkedList2;
        return true;
    }

    public LinkedList<Node> find3(){

        long time1=new Date().getTime();
        System.out.println(time1);
        find();
        find2();

        long time2=new Date().getTime();
        System.out.println(time2);
        System.out.println(time2-time1);
        return linkedList;
    }


    public void show(){
        for (Node temp: linkedList) {
            System.out.println(" "+temp.getX()+"   "+temp.getY() +" ");
        }
    }

    public static void main(String[] args) {
        DfsMap dfsMap=new DfsMap(10,10);
        dfsMap.makeMap();
        dfsMap.showMap();
        BFS bfs=new BFS(dfsMap);




        System.out.println("-------------------------");


        bfs.find3();

        bfs.show();
    }
}

八皇后问题

• 代码实现
• 测试运行

public class Queen {
    static int n=8;//皇后数量
    static int x[]={0,0,0,0,0,0,0,0,0};//x[t]=i 就是皇后放在t行i列
    static int sum;//可行方案数

    private static boolean place (int k)
    {
        for (int j=1;j<k;j++)
            if ((Math.abs(k-j)==Math.abs(x[j]-x[k]))||(x[j]==x[k])) return false;
        return true;
    }

    private static void backtrack (int t) {
        if (t > n) sum++;       //sum是可行方案的个数
        else
            for (int i = 1; i <= n; i++) {
                x[t] = i;
                if (place(t)) backtrack(t + 1);
            }
    }

    public static void main(String[] args) {
        Queen queen=new Queen();
        backtrack(0);
        System.out.println("可行方案数："+sum);
    }
}